In the adjoining figure, explain how one can find the breadth of the river without crossing it.

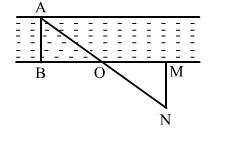
Let AB be the breadth of the river.
M is any point situated on the bank of the river.
Let O be the mid point of BM.

Moving along perpendicular to point such that A,O and N are in a straight line.

Then MN is the required breadth of the river.

In $\triangle \mathrm{OBA}$ and $\triangle \mathrm{OMN}$, we have:

$\mathrm{OB}=\mathrm{OM} \quad(\mathrm{O}$ is midpoint $)$

$\angle \mathrm{OBA}=\angle \mathrm{OMN} \quad\left(\right.$ Each $\left.90^{\circ}\right)$

$\angle \mathrm{AOB}=\angle \mathrm{NOM} \quad($ Vertically opposite angle $)$

$\therefore \triangle \mathrm{OBA} \cong \triangle \mathrm{OMN} \quad$ (ASA criterion)

Thus, MN = AB (CPCT)
If MN is known, one can measure the width of the river without actually crossing it.