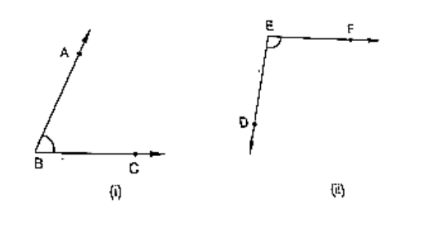
In the below fig, arms BA and BC of ABC are respectively parallel to arms ED and EF of DEF Prove that ∠ABC + ∠DEP = 180°

Given:

AB ∥ DE, BC ∥ EF

To prove: ∠ABC + ∠DEF = 180°

Construction: Produce BC to intersect DE at M

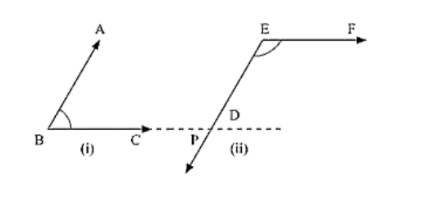
Proof:

Since AB || EM and BL is the transversal

∠ABC = ∠EML         [Corresponding angle] ... (i)

Also,

EF || ML and EM is the transversal

By the property of co-interior angles are supplementary

∠DEF + ∠EML = 180°  ....  (ii)

From (i) and (ii) we have

Therefore ∠DEF + ∠ABC = 180°