In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.

Solution:

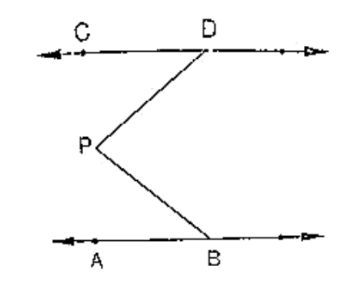
Given that AB ∥ CD

Let EF be the parallel line to AB and CD which passes through P

It can be seen from the figure

Alternative angles are equal

∠ABP = ∠BPF

Alternative angles are equal

∠CDP = ∠DPF

∠ABP + ∠CDP = ∠BPF + ∠DPF

∠ABP + ∠CDP = ∠DPB

Hence proved

AB parallel to CD, P is any point

To prove: ∠ABP + ∠BPD + ∠CDP = 360°

Construction: Draw EF ∥ AB passing through P

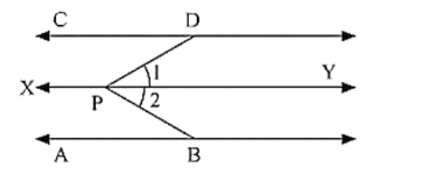
Proof:

Since AB ∥ EF and AB ∥ CD, Therefore EF ∥ CD [Lines parallel to the same line are parallel to each other)

∠ABP + ∠EPB = 180° [Sum of co-interior angles is 180)

∠EPD + ∠COP = 180° ....(1) [Sum of co-interior angles is 180)

∠EPD + ∠CDP = 180°  ....(2)

By adding (1) end (2)

∠ABP + ∠EPB + ∠EPD + ∠CDP = (180 + 180)°

∠ABP + ∠EPB + ∠COP = 360°