In the centre of a rectangular lawn

Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 mx 40 m So, the distance between pond

and lawn would be same around the pond. Say x m.

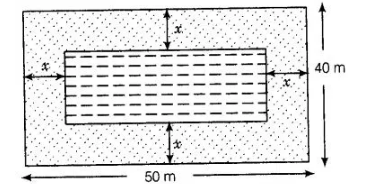
Now, length of rectangular lawn (l1) = 50 m and breadth of rectangular lawn (b1) = 40 m Length of rectangular pond (l2)= 50 – (x + x) = 50 – 2x

and breadth of rectangular pond (b2) = 40 – (x+ x)= 40-2x

Also, area of the grass surrounding the pond =1184 m2

Area of rectangular lawn – Area of rectangular pond

$=$ Area of grass surrounding the pond

$4 \times b_{1}-b_{2} \times b_{2}=1184 \quad[\because$ area of rectangle $=$ length $\times$ breadth $]$

$\Rightarrow \quad 50 \times 40-(50-2 x)(40-2 x)=1184$

$\Rightarrow \quad 2000-\left(2000-80 x-100 x+4 x^{2}\right)=1184$

$\Rightarrow \quad 80 x+100 x-4 x^{2}=1184$

$\Rightarrow \quad 4 x^{2}-180 x+1184=0$

$\Rightarrow \quad x^{2}-45 x+296=0$

$\Rightarrow \quad x^{2}-37 x-8 x+296=0$ [by splitting the middle term]

$\Rightarrow \quad x(x-37)-8(x-37)=0$

$\Rightarrow \quad(x-37)(x-8)=0$

∴                                                                  x=8

[At x = 37, length and breadth of pond are -24 and -34, respectively but length and

breadth cannot be negative. So, x = 37 cannot be possible]

∴                                         Length of pond = 50- 2x= 50- 2 (8)= 50- 16= 34 m

and                             breadth of pond = 40 – 2x = 40 – 2(8) = 40 – 16 = 24 m                       ‘

Hence, required length and breadth of pond are 34 m and 24 m, respectively.