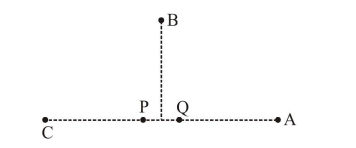
In the figure below, $\mathrm{P}$ and $\mathrm{Q}$ are two equally intense coherent sources emitting radiation of wavelength $20 \mathrm{~m}$. The separation between $\mathrm{P}$ and $Q$ is $5 \mathrm{~m}$ and the phase of $P$ is ahead of that of $\mathrm{Q}$ by $90^{\circ} . \mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three distinct points of observation, each equidistant from the midpoint of PQ. The intensities of radiation at $A, B, C$ will be in the ratio:
Correct Option: , 4
For (A)
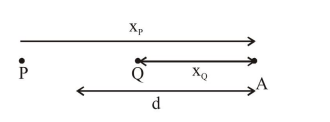
$\mathrm{x}_{\mathrm{P}}-\mathrm{x}_{\mathrm{Q}}=(\mathrm{d}+2.5)-(\mathrm{d}-2.5)$
$=5 \mathrm{~m}$
$\Delta \phi$ due to path difference $=\frac{2 \pi}{\lambda}(\Delta \mathrm{x})=\frac{2 \pi}{20}(5)$
$=\frac{\pi}{2}$
At $A, Q$ is ahead of $P$ by path, as wave emitted by $Q$ reaches before wave emitted by $P$. Total phase difference at $\mathrm{A}$
$=\frac{\pi}{2}-\frac{\pi}{2}$ (due to P being ahead of Q by $90^{\circ}$ )
$=0$
$\mathrm{I}_{\mathrm{A}}=\mathrm{I}_{1}+\mathrm{I}_{2}+2 \sqrt{\mathrm{I}_{1}} \sqrt{\mathrm{I}_{2}} \cos \Delta \phi$
$=\mathrm{I}+\mathrm{I}+2 \sqrt{\mathrm{I}} \sqrt{\mathrm{I}} \cos (0)$
$=4 \mathrm{I}$
For $\mathrm{C}$
$x_{Q}-x_{P}=5 m$
$\Delta \phi$ due to path difference $=\frac{2 \pi}{\lambda}(\Delta x)$
$=\frac{2 \pi}{20}(5)=\frac{\pi}{2}$
Total phase difference at $\mathrm{C}=\frac{\pi}{2}+\frac{\pi}{2}=\pi$
$\mathrm{I}_{\text {net }}=\mathrm{I}_{1}+\mathrm{I}_{2}+2 \sqrt{\mathrm{I}} \sqrt{\mathrm{I}_{2}} \cos (\Delta \phi)$
$=\mathrm{I}+\mathrm{I}+2 \sqrt{\mathrm{I}} \sqrt{\mathrm{I}} \cos (\pi)=0$
For B
$x_{P}-x_{Q}=0$
$\Delta \phi=\frac{\pi}{2}$ (Due to $\mathrm{P}$ being ahead of $\mathrm{Q}$ by $90^{\circ}$ )
$\mathrm{I}_{\mathrm{B}}=\mathrm{I}+\mathrm{I}+2 \sqrt{\mathrm{I}} \sqrt{\mathrm{I}} \cos \frac{\pi}{2}=2 \mathrm{I}$
$\mathrm{I}_{\mathrm{A}}: \mathrm{I}_{\mathrm{B}}: \mathrm{I}_{\mathrm{C}}=4 \mathrm{I}: 2 \mathrm{I}: 0$
$=2: 1: 0$
$\therefore$ correct option is (4)
