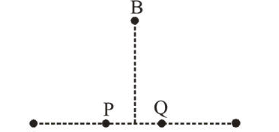
In the figure below, $\mathrm{P}$ and $\mathrm{Q}$ are two equally intense coherent sources emitting radiation of wavelength $20 \mathrm{~m}$. The separation between $P$ and $Q$ is $5 \mathrm{~m}$ and the phase of $P$ is ahead of that of Q by $90^{\circ} . \mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three distinct points of observation, each equidistant from the midpoint of PQ. The intensities of radiation at $\mathrm{A}, \mathrm{B}, \mathrm{C}$ will be in the ratio :
Correct Option: , 2
(2) For (A)
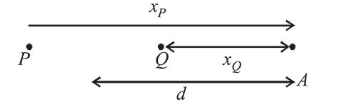
$x_{P}-x_{Q}=(d+2.5)-(d-2.5)=5 \mathrm{~m}$
Phase difference $\Delta \phi$ due to path difference
$=\frac{2 \pi}{\lambda}(\Delta x)=\frac{2 \pi}{20}(5)=\frac{\pi}{2}$
At $A, Q$ is ahead of $P$ by path, as wave emitted by $Q$ reaches before wave emitted by $P$.
$\therefore$ Total phase difference at $A \frac{\pi}{2}-\frac{\pi}{2}=0$
(due to $P$ being ahead of $Q$ by $90^{\circ}$ )
$I_{A}=I_{1}+I_{2}+2 \sqrt{I_{1}} \sqrt{I_{2}} \cos \Delta \phi$
$=I+I+2 \sqrt{I} \sqrt{I} \cos (0)=4 I$
For $C$,
Path difference, $x_{Q}-x_{P}=5 \mathrm{~m}$
Phase difference $\Delta \phi$ due to path difference
$=\frac{2 \pi}{\lambda}(\Delta x)=\frac{2 \pi}{20}(5)=\frac{\pi}{2}$
Total phase difference at $C=\frac{\pi}{2}+\frac{\pi}{2}=\pi$
$I_{\text {net }}=I_{1}+I_{2}+2 \sqrt{I_{1}} \sqrt{I_{2}} \cos (\Delta \phi)$
$=I+I+2 \sqrt{I} \sqrt{I} \cos (\pi)=0$
For $B$,
Path difference, $x_{P}-x_{Q}=0$
Phase difference, $\Delta \phi=\frac{\pi}{2}$
(due to $P$ being ahead of $Q$ by $90^{\circ}$ )
$I_{B}=I+I+2 \sqrt{I} \sqrt{I} \cos \frac{\pi}{2}=2 I$
Therefore intensities of radiation at $A, B$ and $C$ will be in the ratio
$I_{A}: I_{B}: I_{C}=4 I: 2 I: 0=2: 1: 0$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.