In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC.
Question.
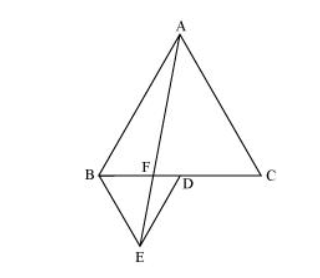
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$
(ii) $\operatorname{ar}(\mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\mathrm{BAE})$
(iii) $\operatorname{ar}(\mathrm{ABC})=2 \operatorname{ar}(\mathrm{BEC})$
(iv) $\operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD})$
(v) $\operatorname{ar}(\mathrm{BFE})=2 \operatorname{ar}(\mathrm{FED})$
(vi) $\operatorname{ar}(\mathrm{FED})=\frac{1}{8} \operatorname{ar}(\mathrm{AFC})$

(i) $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$
(ii) $\operatorname{ar}(\mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\mathrm{BAE})$
(iii) $\operatorname{ar}(\mathrm{ABC})=2 \operatorname{ar}(\mathrm{BEC})$
(iv) $\operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD})$
(v) $\operatorname{ar}(\mathrm{BFE})=2 \operatorname{ar}(\mathrm{FED})$
(vi) $\operatorname{ar}(\mathrm{FED})=\frac{1}{8} \operatorname{ar}(\mathrm{AFC})$
Solution:
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).
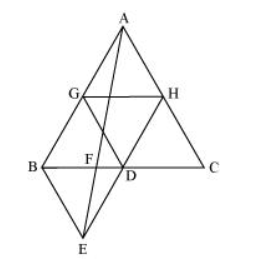
$\Rightarrow \mathrm{GH}=\frac{1}{2} \mathrm{BC}$ and $\mathrm{GH} \| \mathrm{BD}$
$\Rightarrow \mathrm{GH}=\mathrm{BD}=\mathrm{DC}$ and $\mathrm{GH} \| \mathrm{BD}(\mathrm{D}$ is the mid-point of $\mathrm{BC})$
Consider quadrilateral GHDB.
$\mathrm{GH} \| \mathrm{BD}$ and $\mathrm{GH}=\mathrm{BD}$
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area $(\Delta B D G)=$ Area $(\Delta H G D)$
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
$\operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{BDG})+\operatorname{ar}(\Delta \mathrm{GDH})+\operatorname{ar}(\Delta \mathrm{DCH})+\operatorname{ar}(\Delta \mathrm{AGH})$
$\operatorname{ar}(\triangle \mathrm{ABC})=4 \times \operatorname{ar}(\triangle \mathrm{BDE})$
Hence, $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$
(ii)Area $(\Delta B D E)=$ Area $(\triangle A E D)($ Common base $D E$ and $D E \| A B)$
Area $(\triangle B D E)$ - Area $(\triangle F E D)=$ Area $(\triangle A E D)-$ Area $(\triangle F E D)$
Area $(\triangle B E F)=$ Area $(\triangle A F D)(1)$
Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ABF})+$ Area $(\triangle \mathrm{AFD})$
Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ABF})+$ Area $(\triangle \mathrm{BEF})[$ From equation $(1)]$
Area $(\Delta \mathrm{ABD})=$ Area $(\Delta \mathrm{AB} \mathrm{E})(2)$
$A D$ is the median in $\triangle A B C$.
$\operatorname{ar}(\Delta \mathrm{ABD})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABC})$
$=\frac{4}{2} \operatorname{ar}(\Delta B D E)$
(Asproved earlier)
$\operatorname{ar}(\Delta \mathrm{ABD})=2 \operatorname{ar}(\triangle \mathrm{BDE})$(3)
From $(2)$ and $(3)$, we obtain
$2 \operatorname{ar}(\triangle B D E)=\operatorname{ar}(\triangle A B E)$
Or, ar $(\Delta \mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABE})$
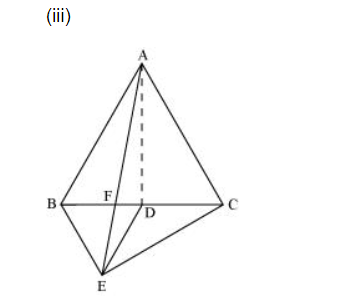
$\operatorname{ar}(\triangle \mathrm{ABE})=\operatorname{ar}(\triangle \mathrm{BEC})($ Common base $\mathrm{BE}$ and $\mathrm{BE} \| \mathrm{AC})$
$\operatorname{ar}(\Delta \mathrm{ABF})+\operatorname{ar}(\Delta \mathrm{BEF})=\operatorname{ar}(\Delta \mathrm{BEC})$
Using equation (1), we obtain
$\operatorname{ar}(\triangle \mathrm{ABF})+\operatorname{ar}(\triangle \mathrm{AFD})=\operatorname{ar}(\triangle \mathrm{BEC})$
$\operatorname{ar}(\triangle \mathrm{ABD})=\operatorname{ar}(\triangle \mathrm{BEC})$
$\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{BEC})$
$\operatorname{ar}(\triangle \mathrm{ABC})=2 \operatorname{ar}(\triangle \mathrm{BEC})$
(iv)It is seen that $\triangle B D E$ and ar $\triangle A E D$ lie on the same base (DE) and between the parallels DE and $A B$.
$\therefore \operatorname{ar}(\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{AED})$
$\Rightarrow \operatorname{ar}(\triangle B D E)-\operatorname{ar}(\triangle F E D)=\operatorname{ar}(\triangle A E D)-\operatorname{ar}(\triangle F E D)$
$\therefore \operatorname{ar}(\Delta \mathrm{BFE})=\operatorname{ar}(\triangle \mathrm{AFD})$
(v) Let $h$ be the height of vertex $E$, corresponding to the side BD in $\triangle B D E$.
Let $H$ be the heiaht of vertex $A$ correspondina to the side $B C \operatorname{in} \triangle A B C$
In (i), it was shown that $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$.
$\therefore \frac{1}{2} \times \mathrm{BD} \times h=\frac{1}{4}\left(\frac{1}{2} \times \mathrm{BC} \times H\right)$
$\Rightarrow \mathrm{BD} \times h=\frac{1}{4}(2 \mathrm{BD} \times H)$
$\Rightarrow h=\frac{1}{2} H$
In (iv) it was shown that $\operatorname{ar}(\Delta B F E)=\operatorname{ar}(\Delta A F D)$.
$=\operatorname{ar}(\mathrm{BFE})+\frac{1}{2} \operatorname{ar}(\mathrm{ABC})$
$[$ In (vi), $\operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD}) ; \mathrm{AD}$ is median of $\triangle \mathrm{ABC}]$
$=\operatorname{ar}(\mathrm{BFE})+\frac{1}{2} \times 4 \operatorname{ar}(\mathrm{BDE})$
$\left[\operatorname{In}(i), \operatorname{ar}(B D E)=\frac{1}{4} \operatorname{ar}(A B C)\right]$
$=\operatorname{ar}(\mathrm{BFE})+2 \operatorname{ar}(\mathrm{BDE})$..(5)
Now, by $(v), \operatorname{ar}(B F E)=2 \operatorname{ar}(F E D) \ldots(6)$
$\operatorname{ar}(\mathrm{BDE})=\operatorname{ar}(\mathrm{BFE})+\operatorname{ar}(\mathrm{FED})=2 \operatorname{ar}(\mathrm{FED})+\operatorname{ar}(\mathrm{FED})=3 \operatorname{ar}(\mathrm{FED})$..(7)
Therefore, from equations $(5),(6)$, and $(7)$, we get:
$\operatorname{ar}(\mathrm{AFC})=2 \operatorname{ar}(\mathrm{FED})+2 \times 3 \operatorname{ar}(\mathrm{FED})=8 \operatorname{ar}(\mathrm{FED})$
$\therefore \operatorname{ar}(\mathrm{AFC})=8 \operatorname{ar}(\mathrm{FED})$
Hence, $\operatorname{ar}(\mathrm{FED})=\frac{1}{8} \operatorname{ar}(\mathrm{AFC})$
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).

$\Rightarrow \mathrm{GH}=\frac{1}{2} \mathrm{BC}$ and $\mathrm{GH} \| \mathrm{BD}$
$\Rightarrow \mathrm{GH}=\mathrm{BD}=\mathrm{DC}$ and $\mathrm{GH} \| \mathrm{BD}(\mathrm{D}$ is the mid-point of $\mathrm{BC})$
Consider quadrilateral GHDB.
$\mathrm{GH} \| \mathrm{BD}$ and $\mathrm{GH}=\mathrm{BD}$
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area $(\Delta B D G)=$ Area $(\Delta H G D)$
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
$\operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{BDG})+\operatorname{ar}(\Delta \mathrm{GDH})+\operatorname{ar}(\Delta \mathrm{DCH})+\operatorname{ar}(\Delta \mathrm{AGH})$
$\operatorname{ar}(\triangle \mathrm{ABC})=4 \times \operatorname{ar}(\triangle \mathrm{BDE})$
Hence, $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$
(ii)Area $(\Delta B D E)=$ Area $(\triangle A E D)($ Common base $D E$ and $D E \| A B)$
Area $(\triangle B D E)$ - Area $(\triangle F E D)=$ Area $(\triangle A E D)-$ Area $(\triangle F E D)$
Area $(\triangle B E F)=$ Area $(\triangle A F D)(1)$
Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ABF})+$ Area $(\triangle \mathrm{AFD})$
Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ABF})+$ Area $(\triangle \mathrm{BEF})[$ From equation $(1)]$
Area $(\Delta \mathrm{ABD})=$ Area $(\Delta \mathrm{AB} \mathrm{E})(2)$
$A D$ is the median in $\triangle A B C$.
$\operatorname{ar}(\Delta \mathrm{ABD})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABC})$
$=\frac{4}{2} \operatorname{ar}(\Delta B D E)$
(Asproved earlier)
$\operatorname{ar}(\Delta \mathrm{ABD})=2 \operatorname{ar}(\triangle \mathrm{BDE})$(3)
From $(2)$ and $(3)$, we obtain
$2 \operatorname{ar}(\triangle B D E)=\operatorname{ar}(\triangle A B E)$
Or, ar $(\Delta \mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABE})$

$\operatorname{ar}(\triangle \mathrm{ABE})=\operatorname{ar}(\triangle \mathrm{BEC})($ Common base $\mathrm{BE}$ and $\mathrm{BE} \| \mathrm{AC})$
$\operatorname{ar}(\Delta \mathrm{ABF})+\operatorname{ar}(\Delta \mathrm{BEF})=\operatorname{ar}(\Delta \mathrm{BEC})$
Using equation (1), we obtain
$\operatorname{ar}(\triangle \mathrm{ABF})+\operatorname{ar}(\triangle \mathrm{AFD})=\operatorname{ar}(\triangle \mathrm{BEC})$
$\operatorname{ar}(\triangle \mathrm{ABD})=\operatorname{ar}(\triangle \mathrm{BEC})$
$\frac{1}{2} \operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{BEC})$
$\operatorname{ar}(\triangle \mathrm{ABC})=2 \operatorname{ar}(\triangle \mathrm{BEC})$
(iv)It is seen that $\triangle B D E$ and ar $\triangle A E D$ lie on the same base (DE) and between the parallels DE and $A B$.
$\therefore \operatorname{ar}(\triangle \mathrm{BDE})=\operatorname{ar}(\triangle \mathrm{AED})$
$\Rightarrow \operatorname{ar}(\triangle B D E)-\operatorname{ar}(\triangle F E D)=\operatorname{ar}(\triangle A E D)-\operatorname{ar}(\triangle F E D)$
$\therefore \operatorname{ar}(\Delta \mathrm{BFE})=\operatorname{ar}(\triangle \mathrm{AFD})$
(v) Let $h$ be the height of vertex $E$, corresponding to the side BD in $\triangle B D E$.
Let $H$ be the heiaht of vertex $A$ correspondina to the side $B C \operatorname{in} \triangle A B C$
In (i), it was shown that $\operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$.
$\therefore \frac{1}{2} \times \mathrm{BD} \times h=\frac{1}{4}\left(\frac{1}{2} \times \mathrm{BC} \times H\right)$
$\Rightarrow \mathrm{BD} \times h=\frac{1}{4}(2 \mathrm{BD} \times H)$
$\Rightarrow h=\frac{1}{2} H$
In (iv) it was shown that $\operatorname{ar}(\Delta B F E)=\operatorname{ar}(\Delta A F D)$.
$=\operatorname{ar}(\mathrm{BFE})+\frac{1}{2} \operatorname{ar}(\mathrm{ABC})$
$[$ In (vi), $\operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD}) ; \mathrm{AD}$ is median of $\triangle \mathrm{ABC}]$
$=\operatorname{ar}(\mathrm{BFE})+\frac{1}{2} \times 4 \operatorname{ar}(\mathrm{BDE})$
$\left[\operatorname{In}(i), \operatorname{ar}(B D E)=\frac{1}{4} \operatorname{ar}(A B C)\right]$
$=\operatorname{ar}(\mathrm{BFE})+2 \operatorname{ar}(\mathrm{BDE})$..(5)
Now, by $(v), \operatorname{ar}(B F E)=2 \operatorname{ar}(F E D) \ldots(6)$
$\operatorname{ar}(\mathrm{BDE})=\operatorname{ar}(\mathrm{BFE})+\operatorname{ar}(\mathrm{FED})=2 \operatorname{ar}(\mathrm{FED})+\operatorname{ar}(\mathrm{FED})=3 \operatorname{ar}(\mathrm{FED})$..(7)
Therefore, from equations $(5),(6)$, and $(7)$, we get:
$\operatorname{ar}(\mathrm{AFC})=2 \operatorname{ar}(\mathrm{FED})+2 \times 3 \operatorname{ar}(\mathrm{FED})=8 \operatorname{ar}(\mathrm{FED})$
$\therefore \operatorname{ar}(\mathrm{AFC})=8 \operatorname{ar}(\mathrm{FED})$
Hence, $\operatorname{ar}(\mathrm{FED})=\frac{1}{8} \operatorname{ar}(\mathrm{AFC})$
