Question.
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
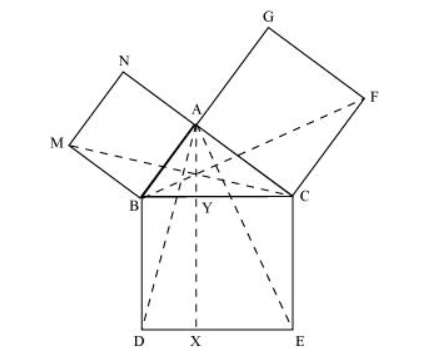
(i) $\triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}$
(ii) $\operatorname{ar}(\mathrm{BYXD})=2 \operatorname{ar}(\mathrm{MBC})$
(iii) $\operatorname{ar}(\mathrm{BYXD})=2 \operatorname{ar}(\mathrm{ABMN})$
(iv) $\Delta \mathrm{FCB} \cong \triangle \mathrm{ACE}$
(v) $\operatorname{ar}(\mathrm{CYXE})=2 \operatorname{ar}(\mathrm{FCB})$
(vi) $\operatorname{ar}(\mathrm{CYXE})=\operatorname{ar}(\mathrm{ACFG})$
(vii) $\operatorname{ar}(\mathrm{BCED})=\operatorname{ar}(\mathrm{ABMN})+\operatorname{ar}(\mathrm{ACFG})$

(i) $\triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}$
(ii) $\operatorname{ar}(\mathrm{BYXD})=2 \operatorname{ar}(\mathrm{MBC})$
(iii) $\operatorname{ar}(\mathrm{BYXD})=2 \operatorname{ar}(\mathrm{ABMN})$
(iv) $\Delta \mathrm{FCB} \cong \triangle \mathrm{ACE}$
(v) $\operatorname{ar}(\mathrm{CYXE})=2 \operatorname{ar}(\mathrm{FCB})$
(vi) $\operatorname{ar}(\mathrm{CYXE})=\operatorname{ar}(\mathrm{ACFG})$
(vii) $\operatorname{ar}(\mathrm{BCED})=\operatorname{ar}(\mathrm{ABMN})+\operatorname{ar}(\mathrm{ACFG})$
Solution:
(i) We know that each angle of a square is $90^{\circ}$.
Hence, $\angle \mathrm{ABM}=\angle \mathrm{DBC}=90^{\circ}$
$\Rightarrow \angle A B M+\angle A B C=\angle D B C+\angle A B C$
$\Rightarrow \angle \mathrm{MBC}=\angle \mathrm{ABD}$
In $\triangle \mathrm{MBC}$ and $\triangle \mathrm{ABD}$,
$\angle \mathrm{MBC}=\angle \mathrm{ABD}($ Proved above $)$
$\mathrm{MB}=\mathrm{AB}$ (Sides of square ABMN)
$B C=B D($ Sides of square BCED $)$
$\therefore \triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}(\mathrm{SAS}$ congruence rule)
(ii) We have
$\triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}$
$\Rightarrow \operatorname{ar}(\Delta \mathrm{MBC})=\operatorname{ar}(\triangle \mathrm{ABD}) \ldots(1)$
It is given that $A X \perp D E$ and $B D \perp D E$ (Adjacent sides of square BDEC)
$\Rightarrow \mathrm{BD} \| \mathrm{AX}$ (Two lines perpendicular to same line are parallel to each other)
$\triangle A B D$ and parallelogram $B Y X D$ are on the same base $B D$ and between the same parallels $B D$ and $A X$.
$\therefore \operatorname{ar}(\triangle \mathrm{ABD})=\frac{1}{2} \operatorname{ar}(\mathrm{BYXD})$
$\operatorname{ar}(B Y X D)=2 \operatorname{ar}(\triangle A B D)$
Area $(B Y X D)=2$ area $(\Delta M B C)[U \operatorname{sing}$ equation $(1)] \ldots(2)$
(iii) $\triangle \mathrm{MBC}$ and parallelogram $\mathrm{ABMN}$ are lying on the same base $\mathrm{MB}$ and between same parallels $\mathrm{MB}$ and $\mathrm{NC}$.
$\therefore \operatorname{ar}(\Delta \mathrm{MBC})=\frac{1}{2} \operatorname{ar}(\mathrm{ABMN})$
$2 \operatorname{ar}(\Delta \mathrm{MBC})=\operatorname{ar}(\mathrm{ABMN})$
$\operatorname{ar}(B Y X D)=\operatorname{ar}(A B M N)[$ Using equation $(2)] \ldots(3)$
(iv) We know that each angle of a square is $90^{\circ}$.
$\therefore \angle \mathrm{FCA}=\angle \mathrm{BCE}=90^{\circ}$
$\Rightarrow \angle \mathrm{FCA}+\angle \mathrm{ACB}=\angle \mathrm{BCE}+\angle \mathrm{ACB}$
$\Rightarrow \angle \mathrm{FCB}=\angle \mathrm{ACE}$
In $\triangle \mathrm{FCB}$ and $\triangle \mathrm{ACE}$,
$\angle F C B=\angle A C E$
$\mathrm{FC}=\mathrm{AC}($ Sides of square $\mathrm{ACF} \mathrm{G})$
$C B=C E($ Sides of square BCED $)$
$\triangle \mathrm{FCB} \cong \triangle \mathrm{ACE}(S A S$ congruence rule $)$
(v) It is given that $A X \perp D E$ and $C E \perp D E$ (Adjacent sides of square BDEC)
Hence, CE II AX (Two lines perpendicular to the same line are parallel to each other)
Consider $\triangle A C E$ and parallelogram $C Y X E$
$\triangle A C E$ and parallelogram $C Y X E$ are on the same base $C E$ and between the same parallels $C E$ and $A X$.
$\therefore \operatorname{ar}(\Delta \mathrm{ACE})=\frac{1}{2} \operatorname{ar}(\mathrm{CYXE})$
$\Rightarrow \operatorname{ar}(C Y X E)=2 \operatorname{ar}(\triangle A C E) \ldots(4)$
We had proved that
$\therefore \triangle \mathrm{FCB} \cong \triangle \mathrm{ACE}$..(5)
On comparing equations (4) and (5), we obtain
$\operatorname{ar}(C Y X E)=2 \operatorname{ar}(\Delta F C B) \ldots(6)$
(vi) Consider $\triangle \mathrm{FCB}$ and parallelogram $\mathrm{ACFG}$
$\triangle \mathrm{FCB}$ and parallelogram $\mathrm{ACFG}$ are lying on the same base $\mathrm{CF}$ and between the same parallels $\mathrm{CF}$ and $\mathrm{BG}$.
$\therefore \operatorname{ar}(\Delta \mathrm{FCB})=\frac{1}{2} \operatorname{ar}(\mathrm{ACFG})$
$\Rightarrow \operatorname{ar}(A C F G)=2 \operatorname{ar}(\Delta F C B)$
$\Rightarrow \operatorname{ar}($ ACFG $)=\operatorname{ar}($ CYXE $)[$ Using equation $(6)] \ldots(7)$
(vii) From the figure, it is evident that
$\operatorname{ar}(B C E D)=\operatorname{ar}(B Y X D)+\operatorname{ar}(C Y X E)$
$\Rightarrow \operatorname{ar}(B C E D)=\operatorname{ar}(A B M N)+\operatorname{ar}(A C F G)[U \operatorname{sing}$ equations $(3)$ and $(7)]$
(i) We know that each angle of a square is $90^{\circ}$.
Hence, $\angle \mathrm{ABM}=\angle \mathrm{DBC}=90^{\circ}$
$\Rightarrow \angle A B M+\angle A B C=\angle D B C+\angle A B C$
$\Rightarrow \angle \mathrm{MBC}=\angle \mathrm{ABD}$
In $\triangle \mathrm{MBC}$ and $\triangle \mathrm{ABD}$,
$\angle \mathrm{MBC}=\angle \mathrm{ABD}($ Proved above $)$
$\mathrm{MB}=\mathrm{AB}$ (Sides of square ABMN)
$B C=B D($ Sides of square BCED $)$
$\therefore \triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}(\mathrm{SAS}$ congruence rule)
(ii) We have
$\triangle \mathrm{MBC} \cong \triangle \mathrm{ABD}$
$\Rightarrow \operatorname{ar}(\Delta \mathrm{MBC})=\operatorname{ar}(\triangle \mathrm{ABD}) \ldots(1)$
It is given that $A X \perp D E$ and $B D \perp D E$ (Adjacent sides of square BDEC)
$\Rightarrow \mathrm{BD} \| \mathrm{AX}$ (Two lines perpendicular to same line are parallel to each other)
$\triangle A B D$ and parallelogram $B Y X D$ are on the same base $B D$ and between the same parallels $B D$ and $A X$.
$\therefore \operatorname{ar}(\triangle \mathrm{ABD})=\frac{1}{2} \operatorname{ar}(\mathrm{BYXD})$
$\operatorname{ar}(B Y X D)=2 \operatorname{ar}(\triangle A B D)$
Area $(B Y X D)=2$ area $(\Delta M B C)[U \operatorname{sing}$ equation $(1)] \ldots(2)$
(iii) $\triangle \mathrm{MBC}$ and parallelogram $\mathrm{ABMN}$ are lying on the same base $\mathrm{MB}$ and between same parallels $\mathrm{MB}$ and $\mathrm{NC}$.
$\therefore \operatorname{ar}(\Delta \mathrm{MBC})=\frac{1}{2} \operatorname{ar}(\mathrm{ABMN})$
$2 \operatorname{ar}(\Delta \mathrm{MBC})=\operatorname{ar}(\mathrm{ABMN})$
$\operatorname{ar}(B Y X D)=\operatorname{ar}(A B M N)[$ Using equation $(2)] \ldots(3)$
(iv) We know that each angle of a square is $90^{\circ}$.
$\therefore \angle \mathrm{FCA}=\angle \mathrm{BCE}=90^{\circ}$
$\Rightarrow \angle \mathrm{FCA}+\angle \mathrm{ACB}=\angle \mathrm{BCE}+\angle \mathrm{ACB}$
$\Rightarrow \angle \mathrm{FCB}=\angle \mathrm{ACE}$
In $\triangle \mathrm{FCB}$ and $\triangle \mathrm{ACE}$,
$\angle F C B=\angle A C E$
$\mathrm{FC}=\mathrm{AC}($ Sides of square $\mathrm{ACF} \mathrm{G})$
$C B=C E($ Sides of square BCED $)$
$\triangle \mathrm{FCB} \cong \triangle \mathrm{ACE}(S A S$ congruence rule $)$
(v) It is given that $A X \perp D E$ and $C E \perp D E$ (Adjacent sides of square BDEC)
Hence, CE II AX (Two lines perpendicular to the same line are parallel to each other)
Consider $\triangle A C E$ and parallelogram $C Y X E$
$\triangle A C E$ and parallelogram $C Y X E$ are on the same base $C E$ and between the same parallels $C E$ and $A X$.
$\therefore \operatorname{ar}(\Delta \mathrm{ACE})=\frac{1}{2} \operatorname{ar}(\mathrm{CYXE})$
$\Rightarrow \operatorname{ar}(C Y X E)=2 \operatorname{ar}(\triangle A C E) \ldots(4)$
We had proved that
$\therefore \triangle \mathrm{FCB} \cong \triangle \mathrm{ACE}$..(5)
On comparing equations (4) and (5), we obtain
$\operatorname{ar}(C Y X E)=2 \operatorname{ar}(\Delta F C B) \ldots(6)$
(vi) Consider $\triangle \mathrm{FCB}$ and parallelogram $\mathrm{ACFG}$
$\triangle \mathrm{FCB}$ and parallelogram $\mathrm{ACFG}$ are lying on the same base $\mathrm{CF}$ and between the same parallels $\mathrm{CF}$ and $\mathrm{BG}$.
$\therefore \operatorname{ar}(\Delta \mathrm{FCB})=\frac{1}{2} \operatorname{ar}(\mathrm{ACFG})$
$\Rightarrow \operatorname{ar}(A C F G)=2 \operatorname{ar}(\Delta F C B)$
$\Rightarrow \operatorname{ar}($ ACFG $)=\operatorname{ar}($ CYXE $)[$ Using equation $(6)] \ldots(7)$
(vii) From the figure, it is evident that
$\operatorname{ar}(B C E D)=\operatorname{ar}(B Y X D)+\operatorname{ar}(C Y X E)$
$\Rightarrow \operatorname{ar}(B C E D)=\operatorname{ar}(A B M N)+\operatorname{ar}(A C F G)[U \operatorname{sing}$ equations $(3)$ and $(7)]$
