In the following figure, $A B C$ is an equilateral triangle of side $8 \mathrm{~cm} . A, B$ and $C$ are the centres of circular arcs of radius $4 \mathrm{~cm}$. Find the area of the shaded region correct upto 2 decimal places. (Take $\pi=3.142$ and $\sqrt{3}=1.732$ ).
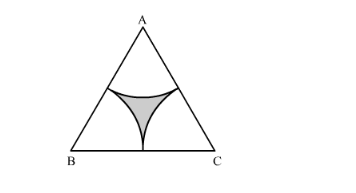
Area of the shaded region can be calculated as shown below,
Area of the shaded region = Area of equilateral triangle − 3 ![]() area of circular arc
area of circular arc
$\therefore$ Area of the shaded region $=\frac{\sqrt{3}}{4} \times 8 \times 8-3 \times \frac{60}{360} \times \pi \times 4 \times 4$
$\therefore$ Area of the shaded region $=\sqrt{3} \times 2 \times 8-3 \times \frac{1}{6} \times \pi \times 4 \times 4$
$\therefore$ Area of the shaded region $=\sqrt{3} \times 16-\frac{1}{2} \times \pi \times 16$
$\therefore$ Area of the shaded region $=\sqrt{3} \times 16-\pi \times 8$
Substituting $\sqrt{3}=1.732$ and $\pi=3.142$ we get,
$\therefore$ Area of the shaded region $=1.732 \times 16-3.142 \times 8$
$\therefore$ Area of the shaded region $=27.712-25.136$
$\therefore$ Area of the shaded region $=2.576$
Therefore, area of the shaded region is $2.576 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
