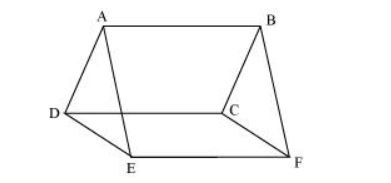
Solution:
It is given that $A B C D$ is a parallelogram. We know that opposite sides of a parallelogram are equal.
$\therefore \mathrm{AD}=\mathrm{BC} \ldots(1)$
Similarly, for parallelograms DCEF and ABFE, it can be proved that
$\mathrm{DE}=\mathrm{CF} \ldots(2)$
And, $E A=F B \ldots(3)$
In $\triangle \mathrm{ADE}$ and $\triangle \mathrm{BCF}$,
AD = BC [Using equation (1)]
DE = CF [Using equation (2)]
EA = FB [Using equation (3)]
$\therefore \triangle \mathrm{ADE} \cong \mathrm{BCF}(\mathrm{SSS}$ congruence rule $)$
$\Rightarrow$ Area $(\triangle \mathrm{ADE})=$ Area $(\triangle \mathrm{BCF})$