In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
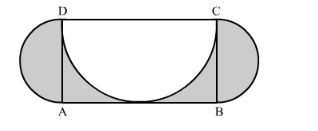
Area of the shaded region can be calculated as shown below,
Area of the shaded region = Area of rectangle − area of the semi-circle with diameter DC triangle + 2 
area of two semicircles with diameters AD and BC
$\therefore$ Area of the shaded region $=7 \times 14-\frac{\pi \times 7^{2}}{2}+2 \times \frac{\pi \times 3.5^{2}}{2}$
$\therefore$ Area of the shaded region $=98-\frac{\pi \times 49}{2}+\pi \times 12.25$
Substituting $\pi=\frac{22}{7}$ we get,
$\therefore$ Area of the shaded region $=98-\frac{\frac{22}{7} \times 49}{2}+\frac{22}{7} \times 12.25$
$\therefore$ Area of the shaded region $=98-\frac{22 \times 7}{2}+22 \times 1.75$
$\therefore$ Area of the shaded region $=98-77+22 \times 1.75$
$\therefore$ Area of the shaded region $=21+38.5$
$\therefore$ Area of the shaded region $=59.5$
Therefore, area of the shaded region is $59.5 \mathrm{~cm}^{2}$