In the following figure, if AC = BD, then prove that AB = CD.

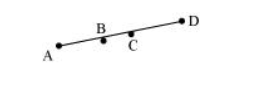
Solution:

From the figure, it can be observed that

$\mathrm{AC}=\mathrm{AB}+\mathrm{BC}$

$B D=B C+C D$

It is given that $A C=B D$

$\mathrm{AB}+\mathrm{BC}=\mathrm{BC}+\mathrm{CD}$(1)

According to Euclid’s axiom, when equals are subtracted from equals, the remainders are also equal.

Subtracting BC from equation (1), we obtain

$\mathrm{AB}+\mathrm{BC}-\mathrm{BC}=\mathrm{BC}+\mathrm{CD}-\mathrm{BC}$

$\mathrm{AB}=\mathrm{CD}$