Question.
In the given figure, $\angle P Q R=100^{\circ}$, where $P, Q$ and $R$ are points on a circle with centre $O$. Find $\angle O P R$.
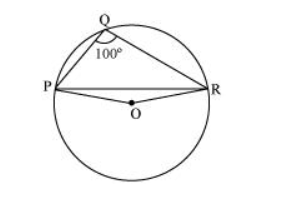
Solution:
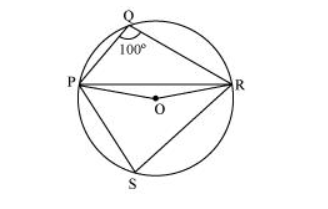
Consider PR as a chord of the circle.
Take any point S on the major arc of the circle.
PQRS is a cyclic quadrilateral.
$\angle \mathrm{PQR}+\angle \mathrm{PSR}=180^{\circ}$ (Opposite angles of a cyclic quadriateral)
$\Rightarrow \angle \mathrm{PSR}=180^{\circ}-100^{\circ}=80^{\circ}$
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\therefore \angle \mathrm{POR}=2 \angle \mathrm{PSR}=2\left(80^{\circ}\right)=160^{\circ}$
In $\triangle \mathrm{POR}$,
OP = OR (Radii of the same circle)
$\therefore \angle O P R=\angle O R P($ Angles opposite to equal sides of a triangle $)$
$\angle O P R+\angle O R P+\angle P O R=180^{\circ}$ (Angle sum property of a triangle)
$2 \angle O P R+160^{\circ}=180^{\circ}$
$2 \angle O P R=180^{\circ}-160^{\circ}=20^{\circ}$
$\angle O P R=10^{\circ}$
Consider PR as a chord of the circle.
Take any point S on the major arc of the circle.
PQRS is a cyclic quadrilateral.
$\angle \mathrm{PQR}+\angle \mathrm{PSR}=180^{\circ}$ (Opposite angles of a cyclic quadriateral)
$\Rightarrow \angle \mathrm{PSR}=180^{\circ}-100^{\circ}=80^{\circ}$
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\therefore \angle \mathrm{POR}=2 \angle \mathrm{PSR}=2\left(80^{\circ}\right)=160^{\circ}$
In $\triangle \mathrm{POR}$,
OP = OR (Radii of the same circle)
$\therefore \angle O P R=\angle O R P($ Angles opposite to equal sides of a triangle $)$
$\angle O P R+\angle O R P+\angle P O R=180^{\circ}$ (Angle sum property of a triangle)
$2 \angle O P R+160^{\circ}=180^{\circ}$
$2 \angle O P R=180^{\circ}-160^{\circ}=20^{\circ}$
$\angle O P R=10^{\circ}$