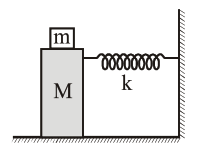
In the given figure, a mass $M$ is attached to a horizontal spring which is fixed on side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period $T$ and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass $m$ is gently fixed upon it. The new amplitude of oscillation will be :
Correct Option: , 2
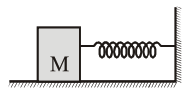
Momentum of system remains conserved.
$\mathrm{p}_{\mathrm{i}}=\mathrm{p}_{\mathrm{f}}$
$\mathrm{MA} \omega=(\mathrm{m}+\mathrm{M}) \mathrm{A}^{\prime} \omega^{\prime}$
$\mathrm{MA} \sqrt{\frac{\mathrm{k}}{\mathrm{M}}}=(\mathrm{m}+\mathrm{M}) \mathrm{A}^{\prime} \sqrt{\frac{\mathrm{k}}{\mathrm{m}+\mathrm{M}}}$
$A^{\prime}=A \sqrt{\frac{M}{M+m}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
