Question:
In the given figure, ∠A = ∠CED, prove that ∆CAB ∼ ∆CED. Also, find the value of x.
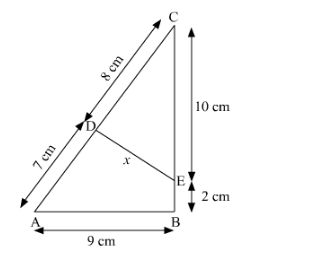
Solution:
Comparing ΔCAB and ΔCED,
∠CAB = ∠CED [Given]
∠ACB = ∠ECD [Common]
$\therefore \triangle C A B \sim \triangle C E D$
$\Rightarrow \frac{C A}{C E}=\frac{A B}{E D}$ [In similar triangles, corresponding sides are in the same proportion]
$\Rightarrow \frac{15 \mathrm{~cm}}{10 \mathrm{~cm}}=\frac{9 \mathrm{~cm}}{x}$
$\Rightarrow x=\frac{9 \times 10}{15} \mathrm{~cm}=6 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
