Question:
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
$[$ Use $\sqrt{3}=1.73, \pi=3.14]$
Solution:
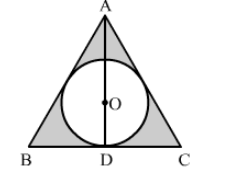
We can find the radius of the incircle by using the formula
$r=\frac{2 \times \text { Area of triangle }}{\text { Perimeter of triangle }}=\frac{2 \times \frac{\sqrt{3}}{4} \times(12)^{2}}{3 \times 12}=2 \sqrt{3} \mathrm{~cm}$
Now, area of shaded region = Area of triangle − Area of circle
$=\frac{\sqrt{3}}{4} \times(12)^{2}-3.14 \times(2 \sqrt{3})^{2}$
$=62.28-37.68$
$=24.6 \mathrm{~cm}^{2}$
Hence, the area of shaded region is 24.6 cm2