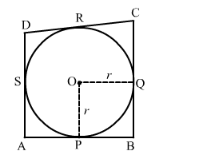
In the given figure, a circle with centre O is inscribed in a quadrilateral ABCD such that,

It is given that the sides BC, AB, AD and CD touches a circle with centre O at points P, Q, R and S, respectively.

AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm.

Now, 

DR = DS = 5 cm           (Lengths of tangents drawn from an external point to a circle are equal)

AR = AD − DR = 23 cm − 5 cm = 18 cm

∴ AQ = AR = 18 cm           (Lengths of tangents drawn from an external point to a circle are equal)

BQ = AB − AQ = 29 cm − 18 cm = 11 cm

∴ BP = BQ = 11 cm           (Lengths of tangents drawn from an external point to a circle are equal)

Now, AB is a tangent at Q and OQ is the radius through the point of contact Q.

$\therefore \angle \mathrm{OQB}=90^{\circ}$   (Tangent at any point of a circle is perpendicular to the radius through the point of contact)

BC is a tangent at P and OP is the radius through the point of contact P.

$\therefore \angle \mathrm{OPB}=90^{\circ} \quad$ (Tangent at any point of a circle is perpendicular to the radius through the point of contact)

$\angle \mathrm{B}=90^{\circ} \quad$ (Given)

Also, BP = BQ

So, OPBQ is a square.

∴ OP = OQ = BQ = 11 cm         (Sides of square are equal)

Thus, the radius of the circle is 11 cm.

Hence, the correct answer is option A.