In the given figure, AB and CD are two parallel chords of a circle. If BDE and ACE are straight lines, intersecting at E,
Question:
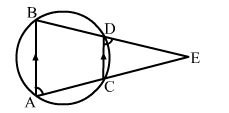
In the given figure, AB and CD are two parallel chords of a circle. If BDE and ACE are straight lines, intersecting at E, prove that ∆AEB is isosceles.
Solution:
AB and CD are two parallel chords of a circle. BDE and ACE are two straight lines that intersect at E.
If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
∴ Exterior ∠EDC = ∠A ...(i)
Exterior ∠DCE = ∠B ...(ii)
Also, AB parallel to CD.
Then, ∠EDC = ∠B (Corresponding angles)
and ∠DCE = ∠A (Corresponding angles)
∴ ∠A = ∠B [From(i) amd (ii)]
Hence, ΔAEB is isosceles.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
