Question:
In the given figure, AB || CD and O is the midpoint of AD.
Show that
(i) ΔAOB ≅ ΔDOC.
(ii) O is the midpoint of BC
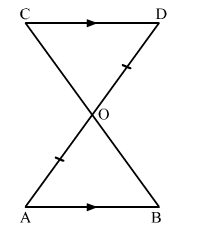
Solution:
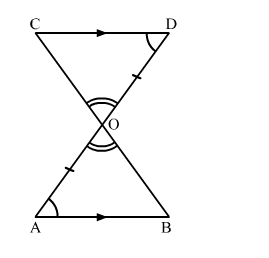
Given: In the given figure, AB || CD and O is the midpoint of AD.
To prove:
(i) ΔAOB ≅ ΔDOC.
(ii) O is the midpoint of BC.
Proof:
(i) In ΔAOB and ΔDOC,
∠BAO = ∠CDO (Alternate interior angles, AB || CD)
AO = DO (Given, O is the midpoint of AD)
∠AOB = ∠DOC (Vertically opposite angles)
∴ By ASA congruence criteria,
ΔAOB ≅ ΔDOC
(ii) ∵ ΔAOB ≅ ΔDOC [From (i)]
∴ BO = CO (CPCT)
Hence, O is the midpoint of BC.
