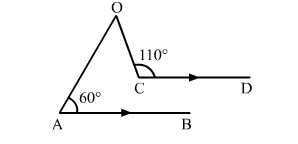
In the given figure, AB || CD. If ∠BAO = 60° and ∠OCD = 110°, then ∠AOC = ?

(c) 50°

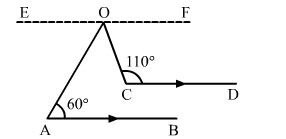
Draw $E O F\|A B\| C D$.

Now, $E O \| A B$ and $O A$ is the transversal.

$\therefore \angle E O A=\angle O A B=60^{\circ} \quad$ [Alternate Interior Angles]

Also,

$O F \| C D$ and $O C$ is the transversal.

$\therefore \angle C O F+\angle O C D=180^{\circ} \quad$ [Angles on the same side of a transversal line are supplementary]

$\Rightarrow \angle C O F+110^{\circ}=180^{\circ}$

$\Rightarrow \angle C O F=70^{\circ}$

Now,

$\angle E O A+\angle A O C+\angle C O F=180^{\circ} \quad[\because E O F$ is a straight line $]$

$\Rightarrow 60^{\circ}+\angle A O C+70^{\circ}=180^{\circ}$

$\Rightarrow \angle A O C=\mathbf{5 0}^{\circ}$