Question:
In the given figure, AB || CD. Prove that ∠BAE − ∠DCE = ∠AEC.
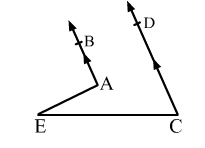
Solution:
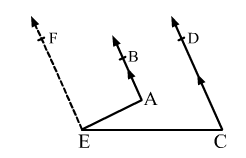
Draw $E F\|A B\| C D$ through $\mathrm{E}$.
Now, $E F \| A B$ and $\mathrm{AE}$ is the transversal.
Then, $\angle B A E+\angle A E F=180^{\circ} \quad$ [Angles on the same side of a transversal line are supplementary]
Again, $E F \| C D$ and $\mathrm{CE}$ is the transversal.
Then
$\angle D C E+\angle C E F=180^{\circ} \quad$ [Angles on the same side of a transversal line are supplementary]
$\Rightarrow \angle D C E+(\angle A E C+\angle A E F)=180^{\circ}$
$\Rightarrow \angle D C E+\angle A E C+180^{\circ}-\angle B A E=180^{\circ}$
$\Rightarrow \angle B A E-\angle D C E=\angle A E C$
