Question:
In the given figure, AB is a chord of a circle with centre O and BOC is a diameter. If OD ⊥ AB such that OD = 6 cm, then AC = ?
(a) 9 cm
(b) 12 cm
(c) 15 cm
(d) 7.5 cm
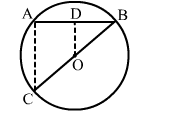
Solution:
(b) 12 cm
OD ⊥ AB
i.e., D is the mid point of AB.
Also, O is the mid point of BC.
Now, in Δ BAC, D is the mid point of AB and O is the mid point of BC.
$\therefore \mathrm{OD}=\frac{1}{2} \mathrm{AC}$ (By mid point theorem)
⇒ AC = 2OD = (2 × 6) cm = 12 cm
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
