In the given figure, ∆ABC is an equilateral triangle the length of whose side is equal to 10 cm,

Solution:

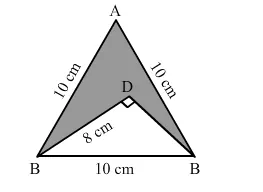
Given:
Side of equilateral triangle ABC = 10 cm
BD = 8 cm

Area of equilateral $\Delta A B C=\frac{\sqrt{3}}{4} \mathrm{a}^{2}$ (where $a=10 \mathrm{~cm}$ )

Area of equilateral $\triangle A B C=\frac{\sqrt{3}}{4} \times 10^{2}$

$=25 \sqrt{3}$

$=25 \times 1.732$

$=43.30 \mathrm{~cm}^{2}$

In the right $\Delta B D C$, we have:

$B C^{2}=B D^{2}+C D^{2}$

$\Rightarrow 10^{2}=8^{2}+C D^{2}$

$\Rightarrow C D^{2}=10^{2}-8^{2}$

$\Rightarrow C D^{2}=36$

$\Rightarrow C D=6$

Area of triangle $\triangle B C D=\frac{1}{2} \times b \times h$

$=\frac{1}{2} \times 8 \times 6$

$=24 \mathrm{~cm}^{2}$

Area of the shaded region = Area of $\Delta A B C-$ Area of $\Delta B D C$

$=43.30-24$

$=19.3 \mathrm{~cm}^{2}$