In the given figure, ∆ABC is right angled at C and DE ⊥ AB.

Solution:

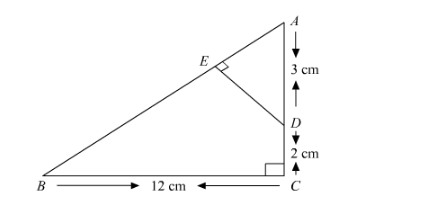
It is given that $A C B$ is right angle triangle and $\angle C=90^{\circ}$

We have to prove that $\triangle A B C \sim \triangle A D E$ and find the lengths of $A E$ and $D E$.

In $\triangle A B C \sim \triangle A D E$

$\angle \mathrm{A}=\angle \mathrm{A} \quad$ Common $\angle \mathrm{C}=\angle \mathrm{E} \quad 90^{\circ}$

So by $A A$ similarly criterion, we have

$\triangle A B C \sim \triangle A D E$

$\Rightarrow \frac{A B}{A D}=\frac{B C}{D E}=\frac{A C}{A E}$

$\Rightarrow \frac{13 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{12 \mathrm{~cm}}{D E}=\frac{5 \mathrm{~cm}}{A E}$

Since

$A B^{2}=A C^{2}+B C^{2}$

$=5^{2}+12^{2}$

$=13^{2}$

So $D E=\frac{36}{13} \mathrm{~cm}$

And $A E=\frac{15}{13} \mathrm{~cm}$

Hence, $D E=\frac{36}{13} \mathrm{~cm}$ and $A E=\frac{15}{13} \mathrm{~cm}$