In the given figure, ABCD and ABPQ are two parallelograms and M is a point on AQ and BMP is a triangle.

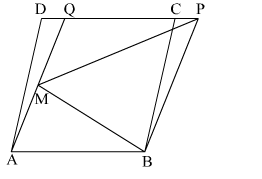
We know parallelogram on the same base and between the same parallels are equal in area. 
Here, AB is the common base and AB || PD
Hence, ar(ABCD) = ar(ABPQ)                             .....(1)
Also, when a triangle and a parallelogram are on the same base and between the same parallels then the
area of triangle is half the area of the parallelogram. 
Here, for the ∆BMP and parallelogrm ABPQ, BP is the common base and they are between the common parallels BP and AQ

So, $\operatorname{ar}(\Delta \mathrm{BMP})=\frac{1}{2} \operatorname{ar}(\| \mathrm{gm} \mathrm{ABPQ})$      .....(2)

From (1) and (2) we have

$\operatorname{ar}(\Delta \mathrm{BMP})=\frac{1}{2} \operatorname{ar}(\| \operatorname{gm} \mathrm{ABCD})$

Thus, the given statement is true.
Hence, the correct answer is option (a).