In the given figure, ABCD is a square and P is a point inside it such that PB = PD. Prove that CPA is a straight line.

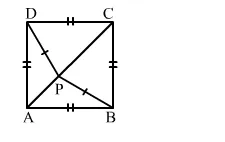
In $\triangle \mathrm{PAD}$ and $\triangle \mathrm{PAB}$, we have :

$\mathrm{AD}=\mathrm{AB} \quad$ (Side of a square)

$\mathrm{AP}=\mathrm{AP} \quad($ Common $)$

$\mathrm{PD}=\mathrm{PB} \quad$ (Given)

$\triangle \mathrm{PAD} \cong \mathrm{PAB} \quad$ (SSS criterion)

$\Rightarrow \angle \mathrm{APD}=\angle \mathrm{APB}$

In $\triangle \mathrm{CPD}$ and $\triangle \mathrm{CPB}$, we have :

$\mathrm{CD}=\mathrm{CB}$ (Sides of square)

$\mathrm{CP}=\mathrm{CP} \quad($ Common $)$

$\mathrm{PD}=\mathrm{PB} \quad$ (Given)

$\triangle \mathrm{CPD} \cong \triangle \mathrm{CPB} \quad(\mathrm{SSS}$ test $)$

$\Rightarrow \angle \mathrm{CPD}=\angle \mathrm{CPB}$

$\therefore \angle \mathrm{APD}+\angle \mathrm{CPD}=\angle \mathrm{APB}+\angle \mathrm{CPB}$

But $\angle \mathrm{APD}+\angle \mathrm{CPD}+\angle \mathrm{APB}+\angle \mathrm{CPB}=360^{\circ}$

$\Rightarrow \angle \mathrm{APD}+\angle \mathrm{CPD}=180^{\circ}$

So, CPA is a straight line.
Hence, proved.