Question:
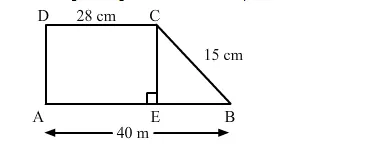
In the given figure ABCD is a trapezium in which AB = 40 m, BC = 15 m, CD = 28 m, AD = 9 m and CE ⊥ AB. Area of trap. ABCD is
(a) 306 m2
(b) 316 m2
(c) 296 m2
(d) 284 m2
Solution:
(a) 306 m2
In the given figure, AECD is a rectangle.
Length AE = Length CD = 28 m
Now
$B E=A B-A E=40-28=12 \mathrm{~m}$
Also,
AD = CE = 9 m
Area of trapezium $=\frac{1}{2} \times$ Sum of parallel sides $\times$ Distance between them
$=\frac{1}{2} \times(D C+A B) \times C E$
$=\frac{1}{2} \times(28+40) \times 9$
$=\frac{1}{2} \times 68 \times 9$
$=306 \mathrm{~m}^{2}$
In the given figure, if DA is perpendicular to AE, then it can be solved, otherwise it cannot be solved.
