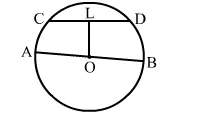
In the given figure, AOB is a diameter of a circle with centre O such that AB = 34 cm and CD is a chord of length 30 cm.
Question:
In the given figure, AOB is a diameter of a circle with centre O such that AB = 34 cm and CD is a chord of length 30 cm. Then the distance of CD from AB is
(a) 8 cm
(b) 15 cm
(c) 18 cm
(d) 6 cm
Solution:
(a) 8 cm
Join OC. Then OC = radius = 17 cm
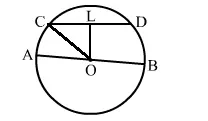
$\mathrm{CL}=\frac{1}{2} \mathrm{CD}=\left(\frac{1}{2} \times 30\right) \mathrm{cm}=15 \mathrm{~cm}$
In right ΔOLC, we have:
$\mathrm{OL}^{2}=\mathrm{OC}^{2}-\mathrm{CL}^{2}=(17)^{2}-(15)^{2}=(289-225)=64$
$\Rightarrow \mathrm{OL}=\sqrt{64}=8 \mathrm{~cm}$
∴ Distance of CD from AB = 8 cm
