In the given figure, ar (DRC) $=\operatorname{ar}(\mathrm{DPC})$ and ar (BDP) $=\operatorname{ar}(\mathrm{ARC})$. Show that both the quadrilaterals $\mathrm{ABCD}$ and $\mathrm{DCPR}$ are trapeziums.

Solution:



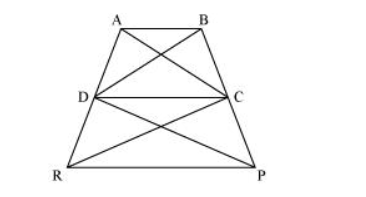
It is given that

Area $(\Delta D R C)=$ Area $(\Delta D P C)$

As $\triangle \mathrm{DRC}$ and $\triangle \mathrm{DPC}$ lie on the same base $\mathrm{DC}$ and have equal areas, therefore, they must lie between the same parallel lines.

$\therefore \mathrm{DC} \| \mathrm{RP}$

Therefore, DCPR is a trapezium.

It is also given that

Area $(\triangle \mathrm{BDP})=$ Area $(\triangle \mathrm{ARC})$

$\Rightarrow$ Area $(B D P)-$ Area $(\Delta D P C)=$ Area $(\Delta A R C)-$ Area $(\Delta D R C)$

$\Rightarrow$ Area $(\Delta B D C)=$ Area $(\Delta A D C)$

Since $\triangle B D C$ and $\triangle A D C$ are on the same base $C D$ and have equal areas, they must lie between the same parallel lines.

$\therefore \mathrm{AB} \| \mathrm{CD}$

Therefore, $A B C D$ is a trapezium.