In the given figure, BC is a tangent to the circle with centre O.

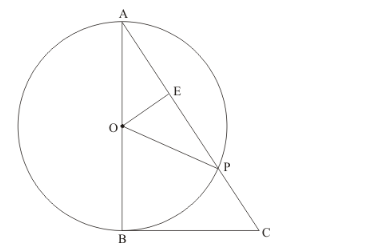
The figure given in the question is below

Let us first take up .

We have,

OA = OP (Since they are the radii of the same circle)

Therefore, is an isosceles triangle. From the property of isosceles triangle, we know that, when a median drawn to the unequal side of the triangle will be perpendicular to the unequal side. Therefore,

Now let us take up  and .

We know that the radius of the circle will always be perpendicular to the tangent at the point of contact. In this problem, OB is the radius and BC is the tangent and B is the point of contact. Therefore,

Also, from the property of isosceles triangle we have found that

Therefore,

=

is the common angle to both the triangles.

Therefore, from AA postulate of similar triangles,

~

Thus we have proved.