Question:
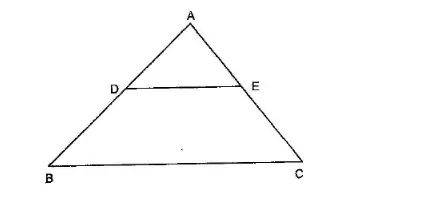
In the given figure, DE || BC and AD=12BD. If BC = 4.5 cm, find DE.
Solution:
Given: In $\triangle A B C, D E \| B C . A D=\frac{1}{2} B D$ and $B C=4.5 \mathrm{~cm}$.
To find: DE
In ∆ABC and ∆ADE
∠B=∠ADE Corresponding angles∠A=∠A Common∴∆ABC~∆ADE AA Similarity
$\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{DE}}{\mathrm{BC}}$
$\frac{\mathrm{AD}}{\mathrm{AD}+\mathrm{BD}}=\frac{\mathrm{DE}}{\mathrm{BC}}$
$\frac{\frac{1}{2} \mathrm{BD}}{\frac{1}{2} \mathrm{BD}+\mathrm{BD}}=\frac{\mathrm{DE}}{\mathrm{BC}}$
$\frac{1}{3}=\frac{\mathrm{DE}}{\mathrm{BC}}$
$\frac{1}{3}=\frac{\mathrm{DE}}{4.5}$
$\mathrm{DE}=1.5 \mathrm{~cm}$
