Question.
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) $\operatorname{ar}(D O C)=\operatorname{ar}(A O B)$
(ii) $\operatorname{ar}(\mathrm{DCB})=\operatorname{ar}(\mathrm{ACB})$
(iii) DA II CB or ABCD is a parallelogram.
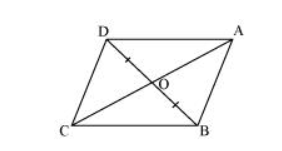
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) $\operatorname{ar}(D O C)=\operatorname{ar}(A O B)$
(ii) $\operatorname{ar}(\mathrm{DCB})=\operatorname{ar}(\mathrm{ACB})$
(iii) DA II CB or ABCD is a parallelogram.

Solution:
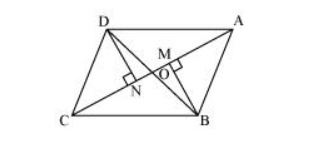
Let us draw $D N \perp A C$ and $B M \perp A C$.
(i) In $\triangle \mathrm{DON}$ and $\triangle \mathrm{BOM}$,
$\angle D N O=\angle B M O$ (By construction)
$\angle D O N=\angle B O M$ (Vertically opposite angles)
$O D=O B$ (Given)
By AAS congruence rule,
$\Delta \mathrm{DON} \cong \triangle \mathrm{BOM}$
$\therefore D N=B M \ldots(1)$
We know that congruent triangles have equal areas.
$\therefore$ Area $(\Delta D O N)=$ Area $(\Delta B O M) \ldots(2)$
In $\triangle D N C$ and $\triangle B M A$,
$\angle D N C=\angle B M A$ (By construction)
$C D=A B$ (Given)
$D N=B M$ [Using equation (1)]
$\therefore \Delta \mathrm{DNC} \cong \Delta \mathrm{BMA}(\mathrm{RHS}$ congruence rule)
$\Rightarrow \operatorname{Area}(\Delta \mathrm{DNC})=\operatorname{Area}(\Delta \mathrm{BMA}) \ldots(3)$
On adding equations $(2)$ and $(3)$, we obtain
Area $(\Delta D O N)+$ Area $(\Delta D N C)=\operatorname{Area}(\Delta B O M)+\operatorname{Area}(\Delta B M A)$
Therefore, Area $(\Delta D O C)=$ Area $(\triangle A O B)$
(ii) We obtained,
Area $(\Delta D O C)=$ Area $(\triangle A O B)$
$\Rightarrow$ Area $(\Delta D O C)+$ Area $(\Delta O C B)=\operatorname{Area}(\Delta A O B)+\operatorname{Area}(\Delta O C B)$
(Adding Area ( $\triangle \mathrm{OCB}$ ) to both sides)
$\Rightarrow$ Area $(\triangle D C B)=$ Area $(\triangle A C B)$
(iii) We obtained,
Area $(\triangle \mathrm{DCB})=$ Area $(\triangle \mathrm{ACB})$
If two triangles have the same base and equal areas, then these will lie between the same parallels.
$\therefore$ DA $\| C B \ldots(4)$
In $\triangle \mathrm{DOA}$ and $\triangle \mathrm{BOC}$,
$\angle D O A=\angle B O C$ (Vertically opposite angles)
$O D=O B($ Given $)$
$\angle O D A=\angle O B C$ (Alternate opposite angles)
By ASA congruence rule,
$\triangle \mathrm{DOA} \cong \triangle \mathrm{BOC}$
$\therefore D A=B C \ldots(5)$
In quadrilateral $A B C D$, one pair of opposite sides is equal and parallel $(A D=B C)$
Therefore, $A B C D$ is a parallelogram.

Let us draw $D N \perp A C$ and $B M \perp A C$.
(i) In $\triangle \mathrm{DON}$ and $\triangle \mathrm{BOM}$,
$\angle D N O=\angle B M O$ (By construction)
$\angle D O N=\angle B O M$ (Vertically opposite angles)
$O D=O B$ (Given)
By AAS congruence rule,
$\Delta \mathrm{DON} \cong \triangle \mathrm{BOM}$
$\therefore D N=B M \ldots(1)$
We know that congruent triangles have equal areas.
$\therefore$ Area $(\Delta D O N)=$ Area $(\Delta B O M) \ldots(2)$
In $\triangle D N C$ and $\triangle B M A$,
$\angle D N C=\angle B M A$ (By construction)
$C D=A B$ (Given)
$D N=B M$ [Using equation (1)]
$\therefore \Delta \mathrm{DNC} \cong \Delta \mathrm{BMA}(\mathrm{RHS}$ congruence rule)
$\Rightarrow \operatorname{Area}(\Delta \mathrm{DNC})=\operatorname{Area}(\Delta \mathrm{BMA}) \ldots(3)$
On adding equations $(2)$ and $(3)$, we obtain
Area $(\Delta D O N)+$ Area $(\Delta D N C)=\operatorname{Area}(\Delta B O M)+\operatorname{Area}(\Delta B M A)$
Therefore, Area $(\Delta D O C)=$ Area $(\triangle A O B)$
(ii) We obtained,
Area $(\Delta D O C)=$ Area $(\triangle A O B)$
$\Rightarrow$ Area $(\Delta D O C)+$ Area $(\Delta O C B)=\operatorname{Area}(\Delta A O B)+\operatorname{Area}(\Delta O C B)$
(Adding Area ( $\triangle \mathrm{OCB}$ ) to both sides)
$\Rightarrow$ Area $(\triangle D C B)=$ Area $(\triangle A C B)$
(iii) We obtained,
Area $(\triangle \mathrm{DCB})=$ Area $(\triangle \mathrm{ACB})$
If two triangles have the same base and equal areas, then these will lie between the same parallels.
$\therefore$ DA $\| C B \ldots(4)$
In $\triangle \mathrm{DOA}$ and $\triangle \mathrm{BOC}$,
$\angle D O A=\angle B O C$ (Vertically opposite angles)
$O D=O B($ Given $)$
$\angle O D A=\angle O B C$ (Alternate opposite angles)
By ASA congruence rule,
$\triangle \mathrm{DOA} \cong \triangle \mathrm{BOC}$
$\therefore D A=B C \ldots(5)$
In quadrilateral $A B C D$, one pair of opposite sides is equal and parallel $(A D=B C)$
Therefore, $A B C D$ is a parallelogram.
