Question.
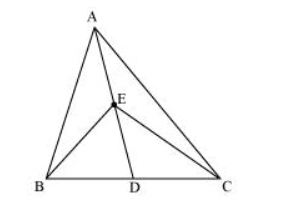
In the given figure, $E$ is any point on median $A D$ of a $\triangle A B C$. Show that $\operatorname{ar}(A B E)=\operatorname{ar}(A C E)$

Solution:
AD is the median of ΔABC. Therefore, it will divide ΔABC into two triangles of equal areas.
$\therefore$ Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ACD}) \ldots(1)$
ED is the median of ΔEBC.
$\therefore$ Area $(\Delta \mathrm{EBD})=$ Area $(\Delta \mathrm{ECD}) \ldots(2)$
On subtracting equation (2) from equation (1), we obtain
Area $(\triangle A B D)$ - Area $(E B D)=$ Area $(\triangle A C D)-$ Area $(\triangle E C D)$
Area $(\triangle \mathrm{ABE})=\operatorname{Area}(\triangle \mathrm{ACE})$
AD is the median of ΔABC. Therefore, it will divide ΔABC into two triangles of equal areas.
$\therefore$ Area $(\triangle \mathrm{ABD})=$ Area $(\triangle \mathrm{ACD}) \ldots(1)$
ED is the median of ΔEBC.
$\therefore$ Area $(\Delta \mathrm{EBD})=$ Area $(\Delta \mathrm{ECD}) \ldots(2)$
On subtracting equation (2) from equation (1), we obtain
Area $(\triangle A B D)$ - Area $(E B D)=$ Area $(\triangle A C D)-$ Area $(\triangle E C D)$
Area $(\triangle \mathrm{ABE})=\operatorname{Area}(\triangle \mathrm{ACE})$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
