In the given figure, find tan P and cot R. Is tan P = cot R?

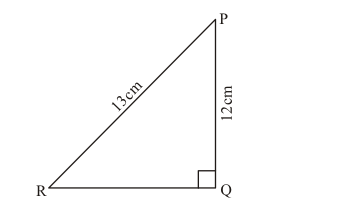
The given figure is below:

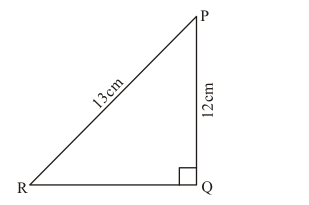
To Find:

$\tan P, \cot R$

In the given right angled ΔPQR, length of side QR is unknown.

Therefore, to find length of side QR we use Pythagoras Theorem

Hence, by applying Pythagoras theorem in ΔPQR,

We get,

$P R^{2}=P Q^{2}+Q R^{2}$

Now, we substitute the length of given side PR and PQ in the above equation

$13^{2}=12^{2}+Q R^{2}$

$Q R^{2}=13^{2}-12^{2}$

$Q R^{2}=169-144$

$O R^{2}=25$

$Q R=\sqrt{25}$

$Q R=5$

By definition, we know that

$\tan P=\frac{\text { Perpendicular side opposite to } \angle \mathrm{P}}{\text { Base side adjacent to } \angle \mathrm{P}}$

$\tan P=\frac{Q R}{P Q}$

$\tan P=\frac{5}{12} \ldots$… (1)

Also, by definition, we know that

$\cot R=\frac{\text { Base side adjacent to } \angle R}{\text { Perpendicular side opposite to } \angle R}$

$\cot R=\frac{Q R}{P Q}$

$\cot R=\frac{5}{12}$...(2)

Comparing equation (1) and (2) , we come to know that R.H.S of both the equation are equal

Therefore, L.H.S of both the equation are also equal

$\tan P=\cot R$

Answer:

Yes, $\tan P=\cot R=\frac{5}{12}$