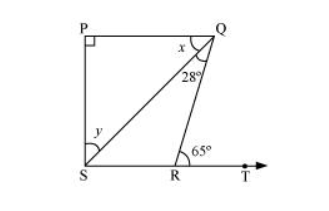
In the given figure, if $P Q \perp P S, P Q \| S R, \angle S Q R=28^{\circ}$ and $\angle Q R T=65^{\circ}$, then find the values of $x$ and $y$.

Solution:

It is given that $P Q \| S R$ and $Q R$ is a transversal line.

$\angle P Q R=\angle Q R T$ (Alternate interior angles)

$x+28^{\circ}=65^{\circ}$

$x=65^{\circ}-28^{\circ}$

$x=37^{\circ}$

By using the angle sum property for $\triangle S P Q$, we obtain

$\angle S P Q+x+y=180^{\circ}$

$90^{\circ}+37^{\circ}+y=180^{\circ}$

$y=180^{\circ}-127^{\circ}$

$y=53^{\circ}$

$\therefore x=37^{\circ}$ and $y=53^{\circ}$