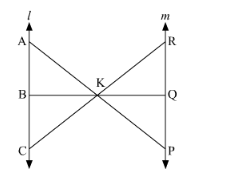
In the given figure, l || m

(i) Three pair of similar triangles are-

$\Delta A B K-\Delta P Q K$(AAA Similarity)

$\Delta C B K-\Delta R Q K$(AAA Similarity)

$\Delta A C K-\Delta P R K$(AAA Similarity)

(ii) Since the pair of similar triangles mentioned above can give us the desired result. The ratios of the corresponding side of the similar triangle are equal.

So,

$\triangle \mathrm{ABK} \approx \triangle \mathrm{PQK}$

Therefore,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AK}}{\mathrm{PK}}=\frac{\mathrm{BK}}{O K} \ldots \ldots$ equation (1)

Similarly in $\triangle \mathrm{CBK} \approx \triangle \mathrm{RQK}$,

$\frac{\mathrm{CB}}{\mathrm{RQ}}=\frac{\mathrm{CK}}{\mathrm{RK}}=\frac{\mathrm{BK}}{Q K}$.... equation (2)

Similarly $\triangle \mathrm{ACK} \approx \Delta \mathrm{PRK}$,

$\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AK}}{\mathrm{PK}}=\frac{\mathrm{CK}}{\mathrm{RK}} \ldots \ldots$ equation (3)

From the above equations 1 and 2 we have,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AK}}{\mathrm{PK}}=\frac{\mathrm{BK}}{Q K}=\frac{\mathrm{CB}}{\mathrm{RQ}}=\frac{\mathrm{CK}}{\mathrm{RK}}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{CB}}{R Q}$ ....eqaution (4)

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{CB}}=\frac{\mathrm{PQ}}{R Q}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{CB}}+\mathrm{l}=\frac{\mathrm{PQ}}{R Q}+1$

$\Rightarrow \frac{\mathrm{AC}}{\mathrm{CB}}=\frac{\mathrm{PR}}{R Q}$

Combining it with equation (4)

$\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{CB}}{R Q}=\frac{A B}{P Q}$

hence proved

$\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{RQ}}$