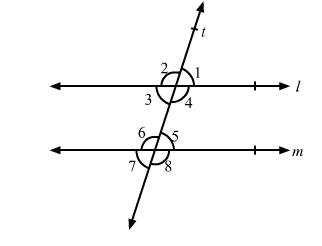
In the given figure, l || m and a transversal t cuts them. If ∠1 : ∠2 = 2 : 3, find the measure of each of the marked angles.
Let ∠1 = 2k and ∠2 = 3k, where k is some constant.
Now, ∠1 and ∠2 form a linear pair.
∴ ∠1 + ∠2 = 180º
⇒ 2k + 3k = 180º
⇒ 5k = 180º
⇒ k = 36º
∴ ∠1 = 2k = 2 × 36º = 72º
∠2 = 3k = 3 × 36º = 108º
Now,
∠3 = ∠1 = 72º (Vertically opposite angles)
∠4 = ∠2 = 108º (Vertically opposite angles)
It is given that, l || m and t is a transversal.
∴ ∠5 = ∠1 = 72º (Pair of corresponding angles)
∠6 = ∠2 = 108º (Pair of corresponding angles)
∠7 = ∠1 = 72º (Pair of alternate exterior angles)
∠8 = ∠2 = 108º (Pair of alternate exterior angles)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
