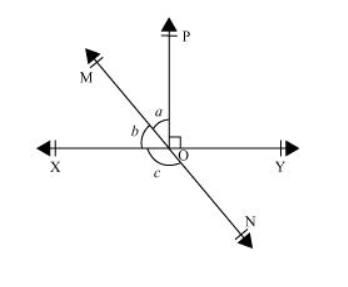
In the given figure, lines $\mathrm{XY}$ and $\mathrm{MN}$ intersect at $\mathrm{O}$. If $\angle \mathrm{POY}=90^{\circ}$ and $a: b=2: 3$, find $c$.

Solution:

Let the common ratio between $a$ and $b$ be $x$.

$\therefore a=2 x$, and $b=3 x$

$X Y$ is a straight line, rays $O M$ and $O P$ stand on it.

$\therefore \angle \mathrm{XOM}+\angle \mathrm{MOP}+\angle \mathrm{POY}=180^{\circ}$

$b+a+\angle \mathrm{POY}=180^{\circ}$

$3 x+2 x+90^{\circ}=180^{\circ}$

$5 x=90^{\circ}$

$x=18^{\circ}$

$a=2 x=2 \times 18=36^{\circ}$

$b=3 x=3 \times 18=54^{\circ}$

MN is a straight line. Ray OX stands on it.

$\therefore b+c=180^{\circ}$ (Linear Pair)

$54^{\circ}+c=180^{\circ}$

$c=180^{\circ}-54^{\circ}=126^{\circ}$

$\therefore c=126^{\circ}$