Question:
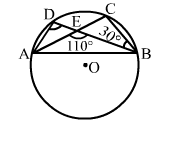
In the given figure, O is the centre of a circle and chords AC and BD intersect at E. If ∠AEB = 110° and ∠CBE = 30°, then ∠ADB = ?
(a) 70°
(b) 60°
(c) 80°
(d) 90°
Solution:
(c) 80°
We have:
∠AEB + ∠CEB = 180° (Linear pair angles)
⇒ 110° + ∠CEB = 180°
⇒ ∠CEB = (180° - 110°) = 70°
In ΔCEB, we have:
∠CEB + ∠EBC + ∠ECB = 180° (Angle sum property of a triangle)
⇒ 70° + 30° + ∠ECB = 180°
⇒ ∠ECB = (180° - 100°) = 80°
The angles in the same segment are equal.
Thus, ∠ADB = ∠ECB = 80°
