In the given figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm.
Question:
In the given figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is
(a) 10 cm
(b) 12 cm
(c) 6 cm
(d) 8 cm
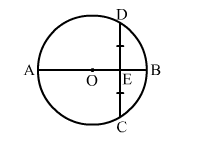
Solution:
(a) 10 cm
Let the radius of the circle be r cm.
Let OD = OB = r cm.
Then OE = (r - 4) cm and ED = 8 cm
Now, in right ΔOED, we have:
$\mathrm{OD}^{2}=\mathrm{OE}^{2}+\mathrm{ED}^{2}$
$\Rightarrow(r)^{2}=(r-4)^{2}+8^{2}$
$\Rightarrow r^{2}=r^{2}+16-8 r+64$
⇒ 8r = 80
⇒ r = 10 cm
Hence, the required radius of the circle is 10 cm.
