In the given figure, O is the centre of the circle and ∠BCO = 30°. Find x and y.

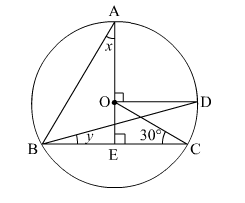
In the given figure, OD is parallel to BC.

∴ ∠BCO = ∠COD    (Alternate interior angles)

$\Rightarrow \angle C O D=30^{\circ}$      

We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it on the remaining part  of the circle.

Here, arc CD subtends ∠COD at the centre and ∠CBD at B on the circle.

∴ ∠COD = 2∠CBD

$\Rightarrow \angle C B D=\frac{30^{\circ}}{2}=15^{\circ}$    (from (1))

$\therefore y=15^{\circ}$            ...(2)

Also, arc AD subtends ∠AOD at the centre and ∠ABD at B on the circle.

∴ ∠AOD = 2∠ABD

$\Rightarrow \angle A B D=\frac{90^{\circ}}{2}=45^{\circ}$        ...(3)

In ∆ABE,
x + y + ∠ABD + ∠AEB = 180∘       (Sum of the angles of a triangle)
⇒  x + 15∘ + 45∘ + 90∘ = 180∘        (from (2) and (3))
⇒  x = 180∘ − (90∘+ 15∘ + 45∘)
⇒  x = 180∘ − 150∘
⇒  x = 30∘

Hence, x = 30∘ and y = 15∘.