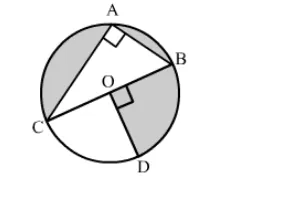
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°.

In right triangle ABC
BC2 = AB2 + AC2  
= (7)2 + (24)2 
= 49 + 576
= 625
∴ BC2 = 625
⇒ BC = 25
Now, ∠COD + ∠BOD = 180°            (Linear pair angles)
⇒∠COD = 180° − 90° = 90°
 Now, Area of the shaded region = Area of sector having central angle (360° − 90°) −  Area of triangle  ABC

$=\frac{270^{\circ}}{360^{\circ}} \pi\left(\frac{\mathrm{BC}}{2}\right)^{2}-\frac{1}{2} \mathrm{AB} \times \mathrm{AC}$

$=\frac{3}{4} \times 3.14\left(\frac{25}{2}\right)^{2}-\frac{1}{2} \times 7 \times 24$

$=367.97-84$

$=283.97 \mathrm{~cm}^{2}$

Hence, the area of shaded region is 283.97 cm2