Question:
In the given figure, ∠OAB = 110° and ∠BCD = 130° then ∠ABC is equal to
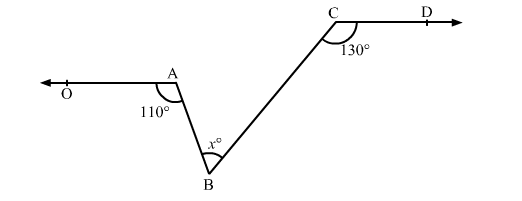
(a) 40°
(b) 50°
(c) 60°
(d) 70°
Solution:
In the given figure, OA || CD.
Construction: Extend OA such that it intersects BC at E.
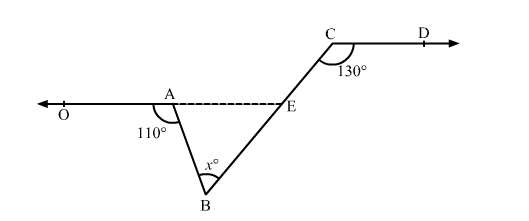
Now, OE || CD and BC is a transversal.
∴ ∠AEC = ∠BCD = 130° (Pair of corresponding angles)
Also, ∠OAB + ∠BAE = 180° (Linear pair)
∴ 110° + ∠BAE = 180°
⇒ ∠BAE = 180° − 110° = 70°
In ∆ABE,
∠AEC = ∠BAE + ∠ABE (In a triangle, exterior angle is equal to the sum of two opposite interior angles)
∴ 130° = 70° + x°
⇒ x° = 130° − 70° = 60°
Thus, the measure of angle ∠ABC is 60°.
Hence, the correct answer is option (c).
