Question:
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
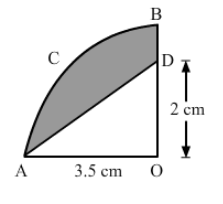
Solution:
Area of the right-angled $\Delta \mathrm{COD}=\frac{1}{2} \times b \times h$
$=\frac{1}{2} \times 3.5 \times 2=3.5 \mathrm{~cm}^{2}$
Area of the sector $\mathrm{AOC}=\frac{\theta}{360} \times \pi \times r^{2}$
$=\frac{90}{360} \times \frac{22}{7} \times(3.5)^{2}$
$=9.625 \mathrm{~cm}^{2}$
Area of the shaded reaion = Area of the $\triangle \mathrm{COD}$ - Area of the sector $\mathrm{AOC}$
$=9.625-3.50$
$=6.125 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
