In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O.

Solution:

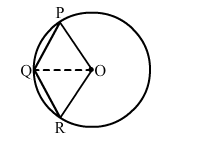
In a rhombus, all sides are congruent to each other.

Thus, we have:

$O P=P Q=Q R=R O$

Now, consider $\Delta Q O P$.

$O Q=O P($ Both are radii. $)$

Therefore, $\Delta Q O P$ is equilateral.

Similarly, $\Delta Q O R$ is also equilateral and $\Delta Q O P \cong \Delta Q O R$.

Ar. $(Q R O P)=\operatorname{Ar} \cdot(\Delta Q O P)+A(\Delta Q O R)=2 \mathrm{Ar} \cdot[\Delta Q O P]$

Ar. $(\Delta \mathrm{QOP})=\frac{1}{2} \times 32 \sqrt{3}=16 \sqrt{3}$

$O r$

$16 \sqrt{3}=\frac{\sqrt{3}}{4} s^{2}$ (where $s$ is the side of the rhombus)

$O r$

$16 \sqrt{3}=\frac{\sqrt{3}}{4} s^{2}$ (where $s$ is the side of the rhombus)

$O r$

$s^{2}=16 \times 4=64$

$\Rightarrow s=8 \mathrm{~cm}$

∴ OQ = 8 cm

Hence, the radius of the circle is 8 cm.