Question.
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) $\operatorname{ar}(A P B)+\operatorname{ar}(P C D)=\frac{1}{2} \operatorname{ar}(A B C D)$
(ii) $\operatorname{ar}(A P D)+\operatorname{ar}(P B C)=\operatorname{ar}(A P B)+\operatorname{ar}(P C D)$
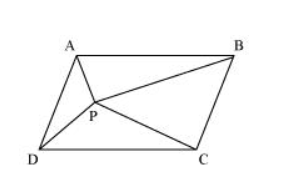
(i) $\operatorname{ar}(A P B)+\operatorname{ar}(P C D)=\frac{1}{2} \operatorname{ar}(A B C D)$
(ii) $\operatorname{ar}(A P D)+\operatorname{ar}(P B C)=\operatorname{ar}(A P B)+\operatorname{ar}(P C D)$
Solution:
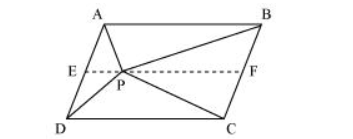
(i) Let us draw a line segment EF, passing through point $P$ and parallel to line segment $A B$.
In parallelogram $A B C D$,
$A B \| E F$ (By construction) ... (1)
ABCD is a parallelogram.
$\therefore A D \| B C$ (Opposite sides of a parallelogram)
$\Rightarrow \mathrm{AE} \| \mathrm{BF} \ldots(2)$
From equations (1) and (2), we obtain
$A B \| E F$ and $A E \| B F$
Therefore, quadrilateral ABFE is a parallelogram.
It can be observed that $\triangle A P B$ and parallelogram $A B F E$ are lying on the same base $A B$ and between the same parallel lines $A B$ and $E F$.
$\therefore$ Area $(\triangle \mathrm{APB})=\frac{1}{2}$ Area $(\mathrm{ABFE})$..(3)
Similarly, for $\triangle P C D$ and parallelogram EFCD,
Area $(\triangle \mathrm{PCD})=\frac{1}{2}$ Area $(\mathrm{EFCD})$..(4)
Adding equations $(3)$ and $(4)$, we obtain
Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})=\frac{1}{2}[$ Area $(\mathrm{ABFE})+$ Area $(\mathrm{EFCD})]$
Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})=\frac{1}{2}$ Area $(\mathrm{ABCD})$..(5)
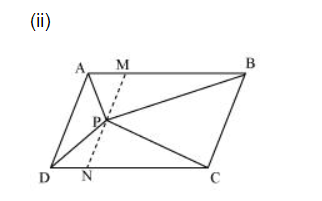
Let us draw a line segment MN, passing through point $P$ and parallel to line segment $A D$.
In parallelogram $A B C D$,
MN $\| A D$ (By construction) $\ldots$ (6)
ABCD is a parallelogram.
$\therefore A B \| D C$ (Opposite sides of a parallelogram)
$\Rightarrow \mathrm{AM} \| \mathrm{DN} \ldots(7)$
From equations $(6)$ and $(7)$, we obtain
MN $\| A D$ and $A M \| D N$
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that $\triangle A P D$ and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
$\therefore$ Area $(\triangle \mathrm{APD})=\frac{1}{2}$ Area (AMND) ...(8)
Similarly, for $\triangle \mathrm{PCB}$ and parallelogram MNCB,
Area $(\triangle \mathrm{PCB})=\frac{1}{2}$ Area $(\mathrm{MNCB})$..(9)
Adding equations (8) and (9), we obtain
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PCB})=\frac{1}{2}[$ Area $(\mathrm{AMND})+$ Area $(\mathrm{MNCB})]$
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PCB})=\frac{1}{2}$ Area $(\mathrm{ABCD})$..(10)
On comparing equations $(5)$ and $(10)$, we obtain
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PBC})=$ Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})$
(i) Let us draw a line segment EF, passing through point $P$ and parallel to line segment $A B$.
In parallelogram $A B C D$,
$A B \| E F$ (By construction) ... (1)
ABCD is a parallelogram.
$\therefore A D \| B C$ (Opposite sides of a parallelogram)
$\Rightarrow \mathrm{AE} \| \mathrm{BF} \ldots(2)$
From equations (1) and (2), we obtain
$A B \| E F$ and $A E \| B F$
Therefore, quadrilateral ABFE is a parallelogram.
It can be observed that $\triangle A P B$ and parallelogram $A B F E$ are lying on the same base $A B$ and between the same parallel lines $A B$ and $E F$.
$\therefore$ Area $(\triangle \mathrm{APB})=\frac{1}{2}$ Area $(\mathrm{ABFE})$..(3)
Similarly, for $\triangle P C D$ and parallelogram EFCD,
Area $(\triangle \mathrm{PCD})=\frac{1}{2}$ Area $(\mathrm{EFCD})$..(4)
Adding equations $(3)$ and $(4)$, we obtain
Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})=\frac{1}{2}[$ Area $(\mathrm{ABFE})+$ Area $(\mathrm{EFCD})]$
Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})=\frac{1}{2}$ Area $(\mathrm{ABCD})$..(5)
Let us draw a line segment MN, passing through point $P$ and parallel to line segment $A D$.
In parallelogram $A B C D$,
MN $\| A D$ (By construction) $\ldots$ (6)
ABCD is a parallelogram.
$\therefore A B \| D C$ (Opposite sides of a parallelogram)
$\Rightarrow \mathrm{AM} \| \mathrm{DN} \ldots(7)$
From equations $(6)$ and $(7)$, we obtain
MN $\| A D$ and $A M \| D N$
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that $\triangle A P D$ and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
$\therefore$ Area $(\triangle \mathrm{APD})=\frac{1}{2}$ Area (AMND) ...(8)
Similarly, for $\triangle \mathrm{PCB}$ and parallelogram MNCB,
Area $(\triangle \mathrm{PCB})=\frac{1}{2}$ Area $(\mathrm{MNCB})$..(9)
Adding equations (8) and (9), we obtain
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PCB})=\frac{1}{2}[$ Area $(\mathrm{AMND})+$ Area $(\mathrm{MNCB})]$
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PCB})=\frac{1}{2}$ Area $(\mathrm{ABCD})$..(10)
On comparing equations $(5)$ and $(10)$, we obtain
Area $(\Delta \mathrm{APD})+$ Area $(\Delta \mathrm{PBC})=$ Area $(\Delta \mathrm{APB})+$ Area $(\Delta \mathrm{PCD})$