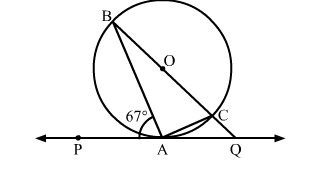
In the given figure, PQ is a tangent to a circle with centre O.

We know that a chord passing through the centre is the diameter of the circle.
∵∠BAC = 90∘    (Angle in a semi circle is 90∘)
By using alternate segment theorem
We have ∠PAB = ∠ACB = 67∘
Now, In △ABC
∠ABC + ∠ACB + ∠BAC = 180∘            [Angle sum property of a triangle]
⇒ ∠ABC + 67∘ +  90∘ = 180∘                      
⇒ ∠ABC= 23∘
Now, ∠BAQ = 180∘ − ∠PAB          [Linear pair angles]
= 180∘ − 67∘
= 113∘
Now, In △ABQ
∠ABQ + ∠AQB + ∠BAQ = 180∘            [Angle sum property of a triangle]
⇒ 23∘ + ∠AQB + 113∘ = 180∘                      
⇒ ∠AQB = 44∘
Hence, the correct answer is option (d).