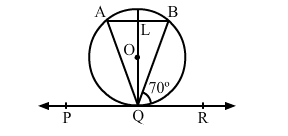
In the given figure, PQR is a tangent to the circle at Q, whose centre is O and AB is a chord parallel to PR,

(c) 40°

Since, $A B \| P R, B Q$ is transversal.

$\angle B Q R=\angle A B Q=70^{\circ}$ [A lternate angles]

$O Q \perp P Q R(\mathrm{~T}$ angents drawn from an external point are perpendicular

to the radius at the point of contact)

and $A B \| P Q R$

$\therefore Q L \perp A B ;$ so, $O L \perp A B$

$\therefore O L$ bisects chord $A B$ [Perpendicular drawn from the centre bisects the chord]

From $\Delta Q L A$ and $\Delta Q L B$ :

$\angle Q L A=\angle Q L B=90^{\circ}$

$L A=L B(O L$ bisects chord $A B)$

$Q L$ is the common side.

$\therefore \Delta Q L A \cong \Delta Q L B[$ By SAS congruency $]$

$\therefore \angle Q A L=\angle Q B L$

$\Rightarrow \angle Q A B=\angle Q B A$

$\therefore \Delta A Q B$ is isosceles.

$\therefore \angle L Q A=\angle L Q R$

$\angle L Q P=\angle L Q R=90^{\circ}$

$\angle L Q B=\left(90^{0}-70^{0}\right)=20^{0}$

$\therefore \angle L Q A=\angle L Q B=20^{\circ}$

$\Rightarrow \angle A Q B=\angle L Q A+\angle L Q B$

$=40^{0}$