In the given figure, ∠Q > ∠R,

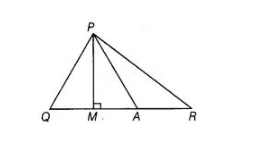
Given In $\triangle P Q R, \angle Q>\angle R, P A$ is the bisector of $\angle Q P R$ and $P M \perp Q R$.

To prove $\angle A P M=\frac{1}{2}(\angle Q-\angle R)$

Proof Since, $P A$ is the bisector of $\angle Q P R$.

$\therefore$ $\angle Q P A=\angle A P R$ $\ldots$ (i)

In $\triangle P Q M$, $\angle P Q M+\angle P M Q+\angle Q P M=180^{\circ}$

[by angle sum property of a triangle]

$\Rightarrow$ $\angle P Q M+90^{\circ}+\angle Q P M=180^{\circ} \quad\left[\because P M \perp Q R \Rightarrow \angle P M Q=90^{\circ}\right]$

$\Rightarrow$  $\angle P Q M=90^{\circ}-\angle Q P M$  ....(ii)

$\ln \Delta P M R_{1}$ 

$\angle P M R+\angle P R M+\angle R P M=180^{\circ}$

[by angle sum property of a triangle]

$\Rightarrow$ $90^{\circ}+\angle P R M+\angle R P M=180^{\circ} \quad\left[\because P M \perp Q R \Rightarrow \angle P M R=90^{\circ}\right]$

$\Rightarrow$ $\angle P R M=180^{\circ}-90^{\circ}-\angle R P M$

$\Rightarrow$ $\angle P R M=90^{\circ}-\angle R P M$ ....(iii)

On subtracting Eq. (iii) from Eq. (ii), we get

$\angle Q-\angle R=\left(90^{\circ}-\angle Q P M\right)-\left(90^{\circ}-\angle R P M\right)$

[where $\angle P Q M=\angle Q$ and $\angle P R M=\angle R$ ]

$\Rightarrow \quad \angle Q-\angle R=\angle R P M-\angle Q P M$

$\Rightarrow \quad \angle Q-\angle R=[\angle R P A+\angle A P M]-[\angle Q P A-\angle A P M]$ ...(iv)

$\Rightarrow \quad \angle Q-\angle R=\angle Q P A+\angle A P M-\angle Q P A+\angle A P M$

[by using Eq. (i)]

$\Rightarrow \quad \angle Q-\angle R=2 \angle A P M$

$\therefore$ $\angle A P M=\frac{1}{2}(\angle Q-\angle R)$

Hence proved.