Question:
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
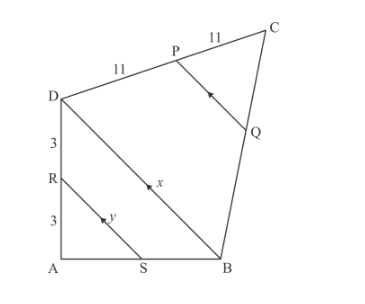
(a) 12, 10
(b) 14, 6
(c) 10, 7
(d) 16, 8
Solution:
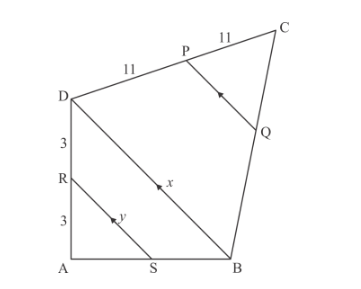
Given: RS || DB || PQ. CP = PD = 11cm and DR = RA = 3cm
To find: the value of x and y respectively.
In ∆ASR and ∆ABD,∠ASR=∠ABQ Corresponding angles∠A=∠A Common∴∆ASR ~∆ABD AA Similarity
$\frac{\mathrm{AR}}{\mathrm{AD}}=\frac{\mathrm{AS}}{\mathrm{AB}}=\frac{\mathrm{RS}}{\mathrm{DB}}$
$\frac{3}{6}=\frac{\text { RS }}{\text { DB }}$
$\frac{1}{2}=\frac{x}{y}$
$x=2 y$
This relation is satisfied by option (d).
Hence, x = 16 cm and y = 8cm
Hence the result is $(d)$.